Question Number 91228 by ~blr237~ last updated on 28/Apr/20
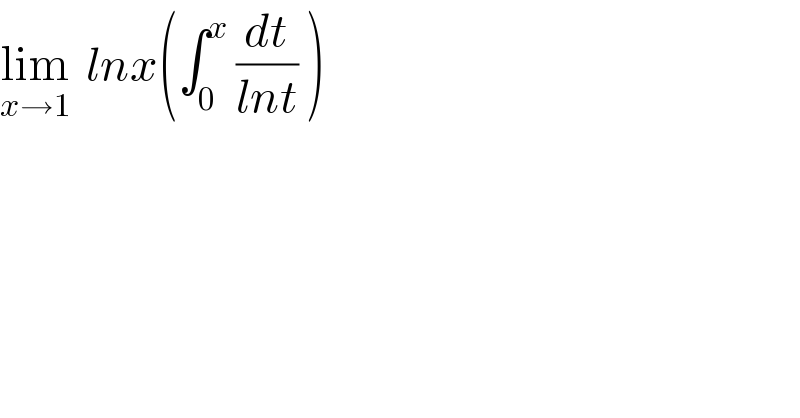
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\:{lnx}\left(\int_{\mathrm{0}} ^{{x}} \:\frac{{dt}}{{lnt}}\:\right)\: \\ $$
Commented by abdomathmax last updated on 29/Apr/20
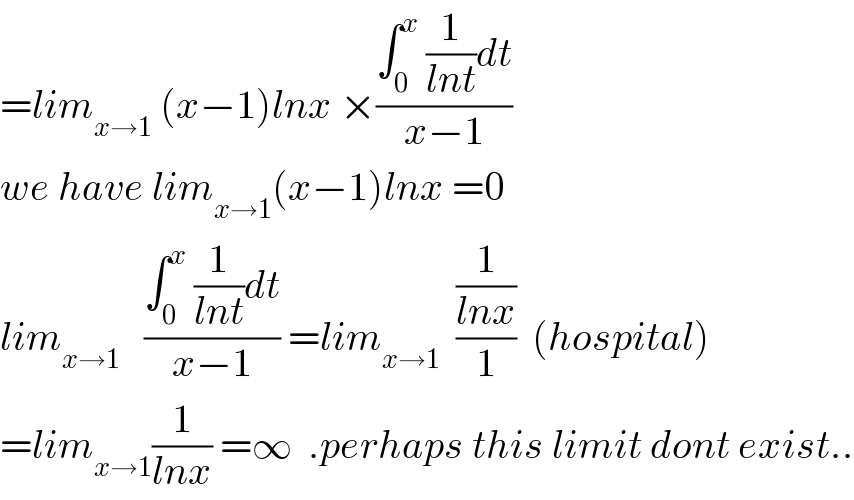
$$={lim}_{{x}\rightarrow\mathrm{1}} \:\left({x}−\mathrm{1}\right){lnx}\:×\frac{\int_{\mathrm{0}} ^{{x}} \:\frac{\mathrm{1}}{{lnt}}{dt}}{{x}−\mathrm{1}} \\ $$$${we}\:{have}\:{lim}_{{x}\rightarrow\mathrm{1}} \left({x}−\mathrm{1}\right){lnx}\:=\mathrm{0} \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} \:\:\:\frac{\int_{\mathrm{0}} ^{{x}} \:\frac{\mathrm{1}}{{lnt}}{dt}}{{x}−\mathrm{1}}\:={lim}_{{x}\rightarrow\mathrm{1}} \:\:\frac{\frac{\mathrm{1}}{{lnx}}}{\mathrm{1}}\:\:\left({hospital}\right) \\ $$$$={lim}_{{x}\rightarrow\mathrm{1}} \frac{\mathrm{1}}{{lnx}}\:=\infty\:\:.{perhaps}\:{this}\:{limit}\:{dont}\:{exist}.. \\ $$
