Question Number 120978 by ZiYangLee last updated on 04/Nov/20
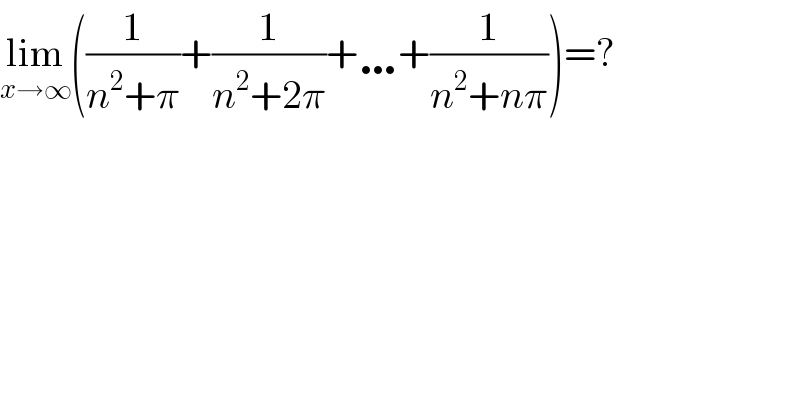
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\pi}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{2}\pi}+\ldots+\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{n}\pi}\right)=? \\ $$
Commented by Dwaipayan Shikari last updated on 04/Nov/20
![If the question becomes lim_(n→∞) ((1/(n+π))+(1/(n+2π))+....+(1/(n+nπ))) lim_(n→∞) (1/n)Σ_(k=1) ^∞ (1/(1+((kπ)/n))) =∫_0 ^1 (1/(1+πx))dx=(1/π)∫_0 ^π (du/(1+u))=(1/π)[log(1+u)]_0 ^π =(1/π)log(1+π)](https://www.tinkutara.com/question/Q121001.png)
$${If}\:{the}\:{question}\:{becomes} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{n}+\pi}+\frac{\mathrm{1}}{{n}+\mathrm{2}\pi}+….+\frac{\mathrm{1}}{{n}+{n}\pi}\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{1}+\frac{{k}\pi}{{n}}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\pi{x}}{dx}=\frac{\mathrm{1}}{\pi}\int_{\mathrm{0}} ^{\pi} \frac{{du}}{\mathrm{1}+{u}}=\frac{\mathrm{1}}{\pi}\left[{log}\left(\mathrm{1}+{u}\right)\right]_{\mathrm{0}} ^{\pi} =\frac{\mathrm{1}}{\pi}{log}\left(\mathrm{1}+\pi\right) \\ $$
Answered by Olaf last updated on 04/Nov/20
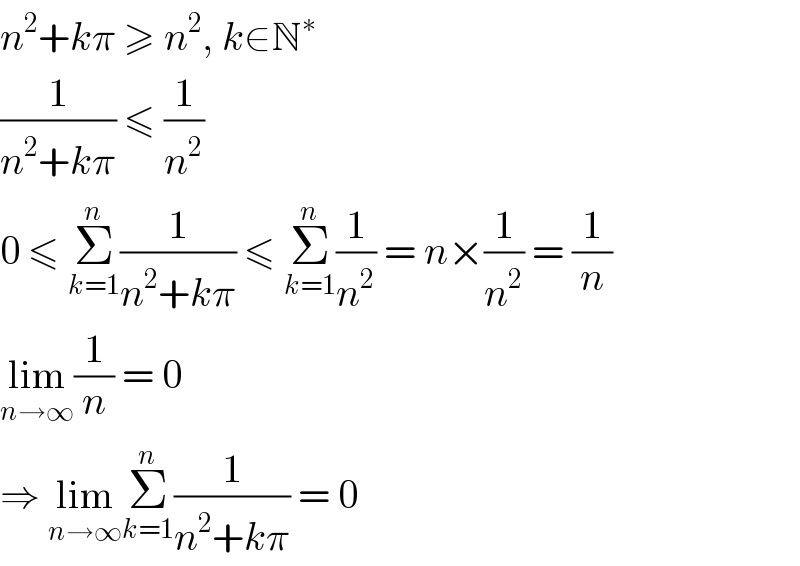
$${n}^{\mathrm{2}} +{k}\pi\:\geqslant\:{n}^{\mathrm{2}} ,\:{k}\in\mathbb{N}^{\ast} \\ $$$$\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{k}\pi}\:\leqslant\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$\mathrm{0}\:\leqslant\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{k}\pi}\:\leqslant\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\:{n}×\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{{n}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{k}\pi}\:=\:\mathrm{0} \\ $$
