Question Number 34982 by rahul 19 last updated on 14/May/18
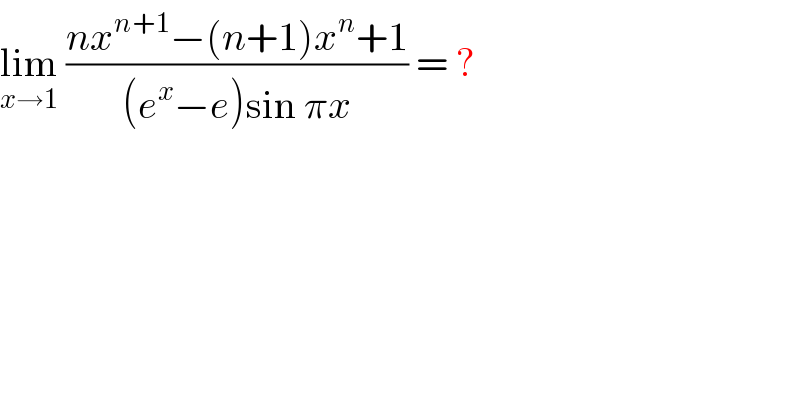
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{nx}^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{{n}} +\mathrm{1}}{\left({e}^{{x}} −{e}\right)\mathrm{sin}\:\pi{x}}\:=\:? \\ $$
Commented by math khazana by abdo last updated on 15/May/18
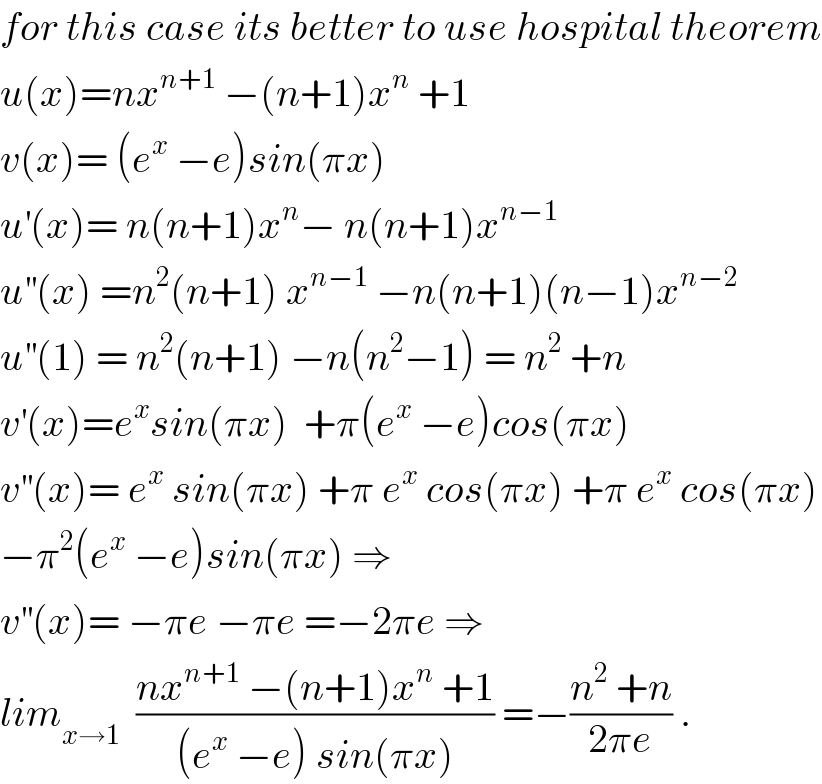
$${for}\:{this}\:{case}\:{its}\:{better}\:{to}\:{use}\:{hospital}\:{theorem} \\ $$$${u}\left({x}\right)={nx}^{{n}+\mathrm{1}} \:−\left({n}+\mathrm{1}\right){x}^{{n}} \:+\mathrm{1} \\ $$$${v}\left({x}\right)=\:\left({e}^{{x}} \:−{e}\right){sin}\left(\pi{x}\right) \\ $$$${u}^{'} \left({x}\right)=\:{n}\left({n}+\mathrm{1}\right){x}^{{n}} −\:{n}\left({n}+\mathrm{1}\right){x}^{{n}−\mathrm{1}} \\ $$$${u}^{''} \left({x}\right)\:={n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)\:{x}^{{n}−\mathrm{1}} \:−{n}\left({n}+\mathrm{1}\right)\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} \\ $$$${u}^{''} \left(\mathrm{1}\right)\:=\:{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)\:−{n}\left({n}^{\mathrm{2}} −\mathrm{1}\right)\:=\:{n}^{\mathrm{2}} \:+{n} \\ $$$${v}^{'} \left({x}\right)={e}^{{x}} {sin}\left(\pi{x}\right)\:\:+\pi\left({e}^{{x}} \:−{e}\right){cos}\left(\pi{x}\right) \\ $$$${v}^{''} \left({x}\right)=\:{e}^{{x}} \:{sin}\left(\pi{x}\right)\:+\pi\:{e}^{{x}} \:{cos}\left(\pi{x}\right)\:+\pi\:{e}^{{x}} \:{cos}\left(\pi{x}\right) \\ $$$$−\pi^{\mathrm{2}} \left({e}^{{x}} \:−{e}\right){sin}\left(\pi{x}\right)\:\Rightarrow \\ $$$${v}^{''} \left({x}\right)=\:−\pi{e}\:−\pi{e}\:=−\mathrm{2}\pi{e}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} \:\:\frac{{nx}^{{n}+\mathrm{1}} \:−\left({n}+\mathrm{1}\right){x}^{{n}} \:+\mathrm{1}}{\left({e}^{{x}} \:−{e}\right)\:{sin}\left(\pi{x}\right)}\:=−\frac{{n}^{\mathrm{2}} \:+{n}}{\mathrm{2}\pi{e}}\:. \\ $$
Commented by rahul 19 last updated on 16/May/18
Thank You prof. Abdo����
Answered by ajfour last updated on 14/May/18
![=lim_(x→1) ((n(n+1)x^(n−1) (x−1))/(e^x sin πx+π(e^x −e)cos πx)) =lim_(x→1) ((n(n+1)x^(n−1) (x−1))/(e^x sin πx+πe(e^(x−1) −1)cos πx)) = ((n(n+1))/(lim_(x→1) ((e^x sin πx)/(x−1))+lim_(x→1) ((πecos πx(e^(x−1) −1))/(x−1)))) =((n(n+1))/(lim_(x→1) ((e^x sin [π+π(x−1)])/(x−1))−πe)) =((n(n+1))/(−2πe)) = ((−n(n+1))/(2πe)) .](https://www.tinkutara.com/question/Q34991.png)
$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\:\frac{{n}\left({n}+\mathrm{1}\right){x}^{{n}−\mathrm{1}} \left({x}−\mathrm{1}\right)}{{e}^{{x}} \mathrm{sin}\:\pi{x}+\pi\left({e}^{{x}} −{e}\right)\mathrm{cos}\:\pi{x}} \\ $$$$\:=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\:\frac{{n}\left({n}+\mathrm{1}\right){x}^{{n}−\mathrm{1}} \left({x}−\mathrm{1}\right)}{{e}^{{x}} \mathrm{sin}\:\pi{x}+\pi{e}\left({e}^{{x}−\mathrm{1}} −\mathrm{1}\right)\mathrm{cos}\:\pi{x}} \\ $$$$=\:\frac{{n}\left({n}+\mathrm{1}\right)}{\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{e}^{{x}} \mathrm{sin}\:\pi{x}}{{x}−\mathrm{1}}+\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\pi{e}\mathrm{cos}\:\pi{x}\left({e}^{{x}−\mathrm{1}} −\mathrm{1}\right)}{{x}−\mathrm{1}}} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)}{\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{e}^{{x}} \mathrm{sin}\:\left[\pi+\pi\left({x}−\mathrm{1}\right)\right]}{{x}−\mathrm{1}}−\pi{e}} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)}{−\mathrm{2}\pi{e}}\:=\:\:\frac{−{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}\pi{e}}\:. \\ $$
Commented by rahul 19 last updated on 14/May/18

$$\mathscr{T}{hank}\:{you}\:{sir}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/May/18
![=((lim)/(x→1))((nx^(n+1) −nx^n −x^n +1)/(e(e^(x−1) −1)sinΠx)) =((lim)/(x→1)) ((nx^n (x−1−(x^n −1))/(e(e^(x−1) −1)sinΠx)) t=x−1 when x→1 t→0 =((lim)/(x→1))((nx^n (x−1)−(x−1)(x^(n−1) +x^(n−2) +....+1))/(e(e^(x−1) −1)sin(Πx))) =((lim)/(x→1 ))((nx^n −(x^(n−1) +x^(n−2) +...1))/(((e(e^(x−1) −1))/(x−1))×sinΠx)) =((lim)/(x→1))((nx^n −(x^(n−1) +x^(n−2) +...+1))/(sinΠx))× ((lim)/(x→1))(1/((e(e^(x−1) −1))/(x−1)))→its value is (1/e) =(1/e)((lim)/(x→1)) ((nx^n −(x^(n−1) +x^(n−2) +...x^(n−(n−1)) +x^(n−n) ))/(sinΠx)) N_r =(1/e)((lim)/(x→1))((n^2 x^(n−1) −{(n−1)x^(n−2) +(n−2)x^(n−3) +..)/) +∣n−(n−1)^� ∣x^(n−(n−1)−1) +0} D_r =((lim)/(x→1))ΠcosΠx so D_r =−Π using l′hospital N_r =(1/e)[n^2 −{(n−1)+(n−2)+(n−3)+...+1} 1=(n−1)+(k−1)×−1 1=n−1−k+1 k=n−1 N_r =(1/e)[n^2 −((n−1)/2)(n−1+1)} =(1/e)[((2n^2 −n^2 +n)/2)] =((n^2 +n)/(2e)) so value ofgiven limit=((n^2 +n)/(−2Πe)) pls check the answer](https://www.tinkutara.com/question/Q34997.png)
$$=\frac{{lim}}{{x}\rightarrow\mathrm{1}}\frac{{nx}^{{n}+\mathrm{1}} −{nx}^{{n}} −{x}^{{n}} +\mathrm{1}}{{e}\left({e}^{{x}−\mathrm{1}} −\mathrm{1}\right){sin}\Pi{x}} \\ $$$$=\frac{{lim}}{{x}\rightarrow\mathrm{1}}\:\frac{{nx}^{{n}} \left({x}−\mathrm{1}−\left({x}^{{n}} −\mathrm{1}\right)\right.}{{e}\left({e}^{{x}−\mathrm{1}} −\mathrm{1}\right){sin}\Pi{x}} \\ $$$${t}={x}−\mathrm{1}\:\:\:{when}\:{x}\rightarrow\mathrm{1}\:\:\:{t}\rightarrow\mathrm{0} \\ $$$$=\frac{{lim}}{{x}\rightarrow\mathrm{1}}\frac{{nx}^{{n}} \left({x}−\mathrm{1}\right)−\left({x}−\mathrm{1}\right)\left({x}^{{n}−\mathrm{1}} +{x}^{{n}−\mathrm{2}} +….+\mathrm{1}\right)}{{e}\left({e}^{{x}−\mathrm{1}} −\mathrm{1}\right){sin}\left(\Pi{x}\right)} \\ $$$$=\frac{{lim}}{{x}\rightarrow\mathrm{1}\:\:}\frac{{nx}^{{n}} −\left({x}^{{n}−\mathrm{1}} +{x}^{{n}−\mathrm{2}} +…\mathrm{1}\right)}{\frac{{e}\left({e}^{{x}−\mathrm{1}} −\mathrm{1}\right)}{{x}−\mathrm{1}}×{sin}\Pi{x}} \\ $$$$=\frac{{lim}}{{x}\rightarrow\mathrm{1}}\frac{{nx}^{{n}} −\left({x}^{{n}−\mathrm{1}} +{x}^{{n}−\mathrm{2}} +…+\mathrm{1}\right)}{{sin}\Pi{x}}× \\ $$$$\frac{{lim}}{{x}\rightarrow\mathrm{1}}\frac{\mathrm{1}}{\frac{{e}\left({e}^{{x}−\mathrm{1}} −\mathrm{1}\right)}{{x}−\mathrm{1}}}\rightarrow{its}\:{value}\:{is}\:\frac{\mathrm{1}}{{e}} \\ $$$$=\frac{\mathrm{1}}{{e}}\frac{{lim}}{{x}\rightarrow\mathrm{1}}\:\frac{{nx}^{{n}} −\left({x}^{{n}−\mathrm{1}} +{x}^{{n}−\mathrm{2}} +…{x}^{{n}−\left({n}−\mathrm{1}\right)} +{x}^{{n}−{n}} \right)}{{sin}\Pi{x}} \\ $$$${N}_{{r}} \\ $$$$=\frac{\mathrm{1}}{{e}}\frac{{lim}}{{x}\rightarrow\mathrm{1}}\frac{{n}^{\mathrm{2}} {x}^{{n}−\mathrm{1}} −\left\{\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} +\left({n}−\mathrm{2}\right){x}^{{n}−\mathrm{3}} +..\right.}{} \\ $$$$\left.+\mid{n}−\left({n}−\mathrm{1}\bar {\right)}\mid{x}^{{n}−\left({n}−\mathrm{1}\right)−\mathrm{1}} +\mathrm{0}\right\} \\ $$$${D}_{{r}} =\frac{{lim}}{{x}\rightarrow\mathrm{1}}\Pi{cos}\Pi{x} \\ $$$${so}\:{D}_{{r}} =−\Pi \\ $$$${using}\:{l}'{hospital} \\ $$$${N}_{{r}} =\frac{\mathrm{1}}{{e}}\left[{n}^{\mathrm{2}} −\left\{\left({n}−\mathrm{1}\right)+\left({n}−\mathrm{2}\right)+\left({n}−\mathrm{3}\right)+…+\mathrm{1}\right\}\right. \\ $$$$\mathrm{1}=\left({n}−\mathrm{1}\right)+\left({k}−\mathrm{1}\right)×−\mathrm{1} \\ $$$$\mathrm{1}={n}−\mathrm{1}−{k}+\mathrm{1} \\ $$$${k}={n}−\mathrm{1} \\ $$$${N}_{{r}} =\frac{\mathrm{1}}{{e}}\left[{n}^{\mathrm{2}} −\frac{{n}−\mathrm{1}}{\mathrm{2}}\left({n}−\mathrm{1}+\mathrm{1}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{{e}}\left[\frac{\mathrm{2}{n}^{\mathrm{2}} −{n}^{\mathrm{2}} +{n}}{\mathrm{2}}\right] \\ $$$$=\frac{{n}^{\mathrm{2}} +{n}}{\mathrm{2}{e}} \\ $$$${so}\:{value}\:{ofgiven}\:{limit}=\frac{{n}^{\mathrm{2}} +{n}}{−\mathrm{2}\Pi{e}} \\ $$$${pls}\:{check}\:{the}\:{answer} \\ $$
Commented by rahul 19 last updated on 14/May/18
$${Absolutely}\:{correct}! \\ $$$$\mathscr{T}{hank}\:{you}\:{sir}. \\ $$
