Question Number 86655 by jagoll last updated on 30/Mar/20
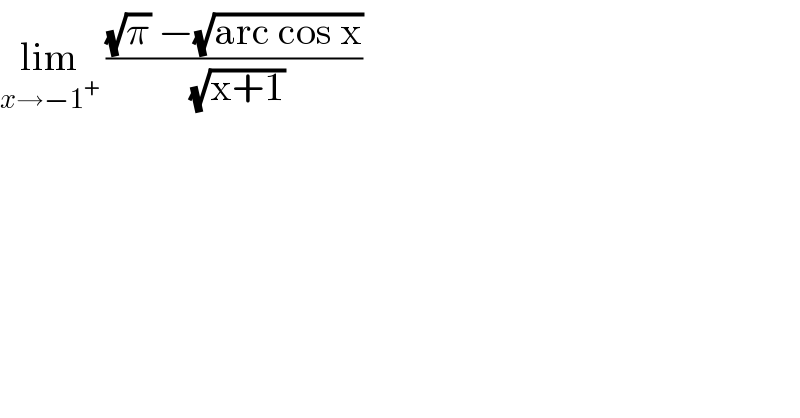
$$\underset{{x}\rightarrow−\mathrm{1}^{+} } {\mathrm{lim}}\:\frac{\sqrt{\pi}\:−\sqrt{\mathrm{arc}\:\mathrm{cos}\:\mathrm{x}}}{\:\sqrt{\mathrm{x}+\mathrm{1}}} \\ $$
Answered by john santu last updated on 30/Mar/20
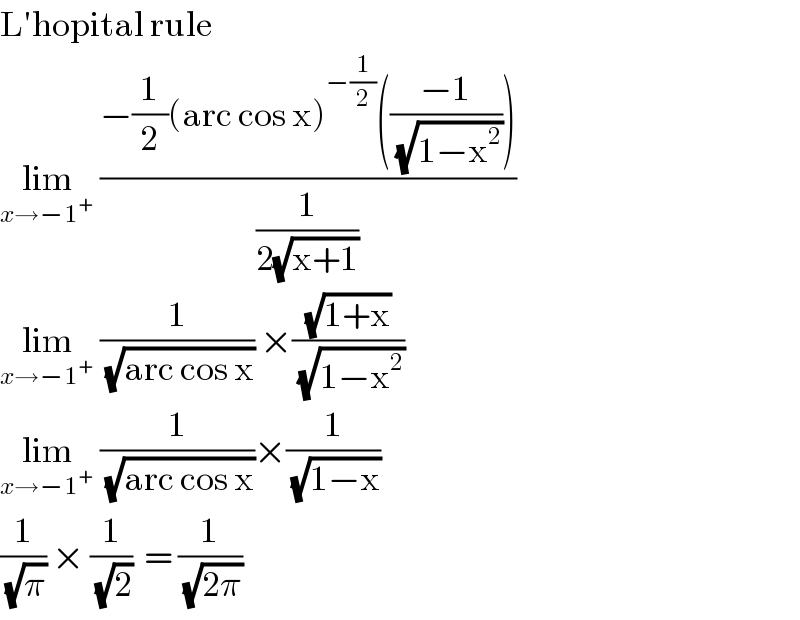
$$\mathrm{L}'\mathrm{hopital}\:\mathrm{rule} \\ $$$$\underset{{x}\rightarrow−\mathrm{1}^{+} } {\mathrm{lim}}\:\frac{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{arc}\:\mathrm{cos}\:\mathrm{x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\frac{−\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\right)}{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}+\mathrm{1}}}}\: \\ $$$$\underset{{x}\rightarrow−\mathrm{1}^{+} } {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{arc}\:\mathrm{cos}\:\mathrm{x}}}\:×\frac{\sqrt{\mathrm{1}+\mathrm{x}}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }} \\ $$$$\underset{{x}\rightarrow−\mathrm{1}^{+} } {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{arc}\:\mathrm{cos}\:\mathrm{x}}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{x}}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\pi}}\:×\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\pi}} \\ $$
Commented by jagoll last updated on 30/Mar/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
