Menu Close

lim-x-1-x-1-1-x-1-3-1-x-2-1-3-

Tinku Tara 0 Comments
Pin




Question Number 91133 by john santu last updated on 28/Apr/20
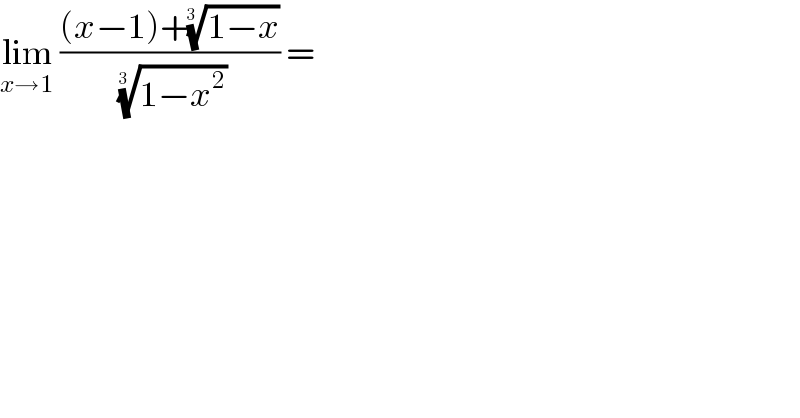
lim_(x→1) (((x−1)+((1−x))^(1/(3 )) )/( ((1−x^2 ))^(1/(3 )) )) =
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left({x}−\mathrm{1}\right)+\sqrt[{\mathrm{3}\:\:}]{\mathrm{1}−{x}}}{\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{1}−{x}^{\mathrm{2}} }}\:=\: \\ $$
Commented by john santu last updated on 28/Apr/20
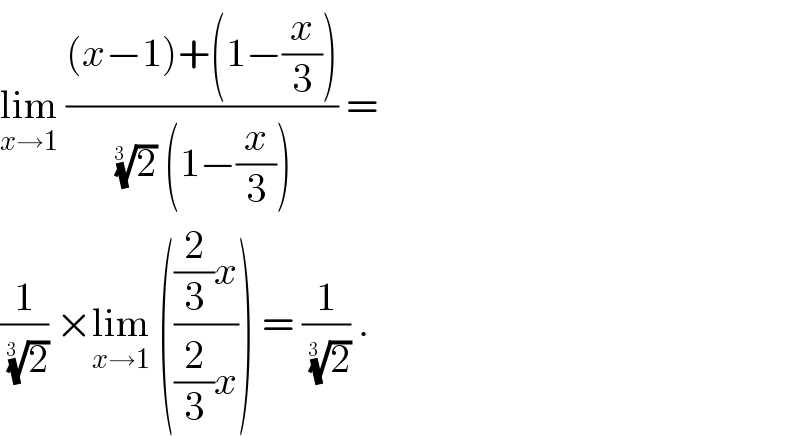
lim_(x→1) (((x−1)+(1−(x/3)))/( (2)^(1/(3 )) (1−(x/3)))) = (1/( (2)^(1/(3 )) )) ×lim_(x→1) ((((2/3)x)/((2/3)x))) = (1/( (2)^(1/(3 )) )) .
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left({x}−\mathrm{1}\right)+\left(\mathrm{1}−\frac{{x}}{\mathrm{3}}\right)}{\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{2}}\:\left(\mathrm{1}−\frac{{x}}{\mathrm{3}}\right)}\:=\: \\ $$$$\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{2}}}\:×\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\frac{\mathrm{2}}{\mathrm{3}}{x}}{\frac{\mathrm{2}}{\mathrm{3}}{x}}\right)\:=\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{2}}}\:.\: \\ $$
Commented by mathmax by abdo last updated on 28/Apr/20
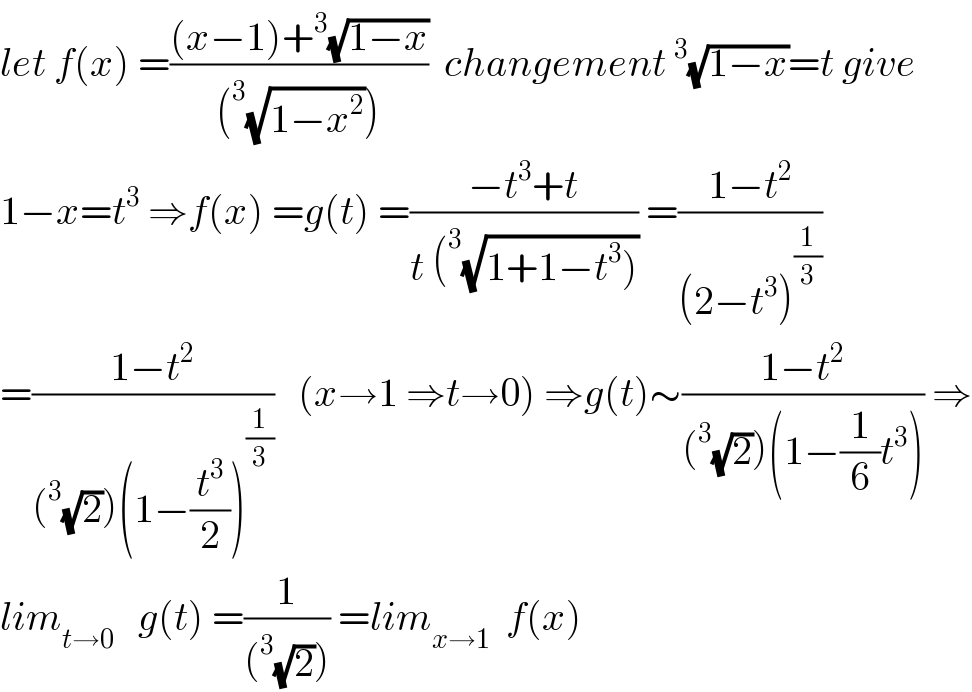
let f(x) =(((x−1)+^3 (√(1−x)))/((^3 (√(1−x^2 ))))) changement^3 (√(1−x))=t give 1−x=t^3 ⇒f(x) =g(t) =((−t^3 +t)/(t (^3 (√(1+1−t^3 ))))) =((1−t^2 )/((2−t^3 )^(1/3) )) =((1−t^2 )/((^3 (√2))(1−(t^3 /2))^(1/3) )) (x→1 ⇒t→0) ⇒g(t)∼((1−t^2 )/((^3 (√2))(1−(1/6)t^3 ))) ⇒ lim_(t→0) g(t) =(1/((^3 (√2)))) =lim_(x→1) f(x)
$${let}\:{f}\left({x}\right)\:=\frac{\left({x}−\mathrm{1}\right)+^{\mathrm{3}} \sqrt{\mathrm{1}−{x}}}{\left(^{\mathrm{3}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)}\:\:{changement}\:^{\mathrm{3}} \sqrt{\mathrm{1}−{x}}={t}\:{give} \\ $$$$\mathrm{1}−{x}={t}^{\mathrm{3}} \:\Rightarrow{f}\left({x}\right)\:={g}\left({t}\right)\:=\frac{−{t}^{\mathrm{3}} +{t}}{{t}\:\left(^{\mathrm{3}} \sqrt{\left.\mathrm{1}+\mathrm{1}−{t}^{\mathrm{3}} \right)}\right.}\:=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left(\mathrm{2}−{t}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$$=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left(^{\mathrm{3}} \sqrt{\mathrm{2}}\right)\left(\mathrm{1}−\frac{{t}^{\mathrm{3}} }{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }\:\:\:\left({x}\rightarrow\mathrm{1}\:\Rightarrow{t}\rightarrow\mathrm{0}\right)\:\Rightarrow{g}\left({t}\right)\sim\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left(^{\mathrm{3}} \sqrt{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}{t}^{\mathrm{3}} \right)}\:\Rightarrow \\ $$$${lim}_{{t}\rightarrow\mathrm{0}} \:\:\:{g}\left({t}\right)\:=\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{\mathrm{2}}\right)}\:={lim}_{{x}\rightarrow\mathrm{1}} \:\:{f}\left({x}\right) \\ $$
Answered by john santu last updated on 28/Apr/20
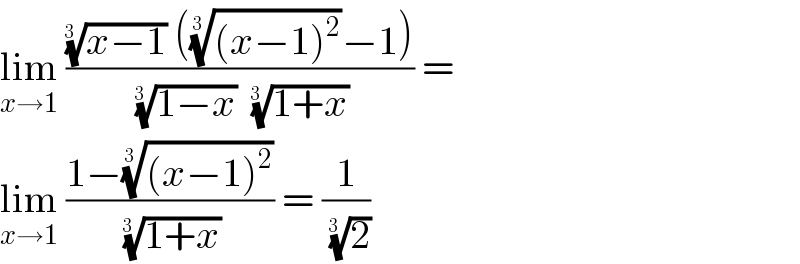
lim_(x→1) ((((x−1))^(1/(3 )) ((((x−1)^2 ))^(1/(3 )) −1))/( ((1−x))^(1/(3 )) ((1+x))^(1/(3 )) )) = lim_(x→1) ((1−(((x−1)^2 ))^(1/(3 )) )/( ((1+x))^(1/(3 )) )) = (1/( (2)^(1/(3 )) ))
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:\:}]{{x}−\mathrm{1}}\:\left(\sqrt[{\mathrm{3}\:\:}]{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{1}\right)}{\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{1}−{x}}\:\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{1}+{x}}}\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}−\sqrt[{\mathrm{3}\:\:}]{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }}{\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{1}+{x}}}\:=\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{2}}}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *