Question Number 159276 by amin96 last updated on 14/Nov/21
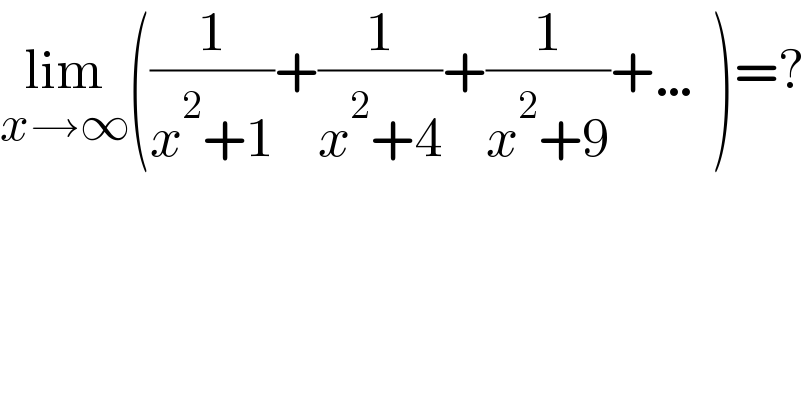
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{4}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{9}}+\ldots\right)=? \\ $$
Answered by Ar Brandon last updated on 14/Nov/21

$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{n}^{\mathrm{2}} }=\mathrm{0} \\ $$
Commented by amin96 last updated on 15/Nov/21

$${answer}\:\:\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right) \\ $$
Commented by Ar Brandon last updated on 15/Nov/21
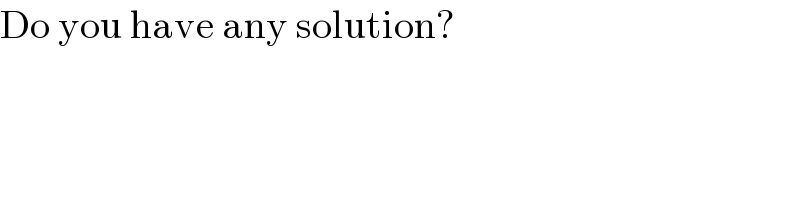
$$\mathrm{Do}\:\mathrm{you}\:\mathrm{have}\:\mathrm{any}\:\mathrm{solution}? \\ $$
Commented by mindispower last updated on 15/Nov/21

$${hint} \\ $$$$\frac{{Sh}\left(\pi{z}\right)}{\pi{z}}=\underset{{n}\geqslant\mathrm{1}} {\prod}\left(\mathrm{1}+\frac{{z}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right) \\ $$
Commented by amin96 last updated on 15/Nov/21

$${solution}??? \\ $$
