Question Number 99938 by bemath last updated on 24/Jun/20
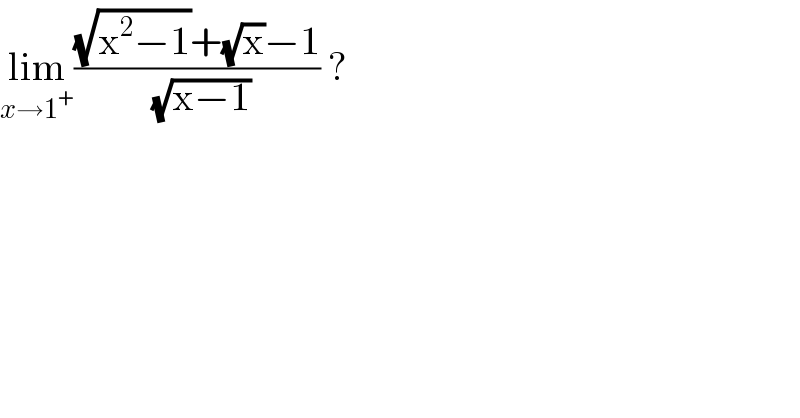
$$\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}+\sqrt{\mathrm{x}}−\mathrm{1}}{\:\sqrt{\mathrm{x}−\mathrm{1}}}\:?\: \\ $$
Commented by bobhans last updated on 24/Jun/20
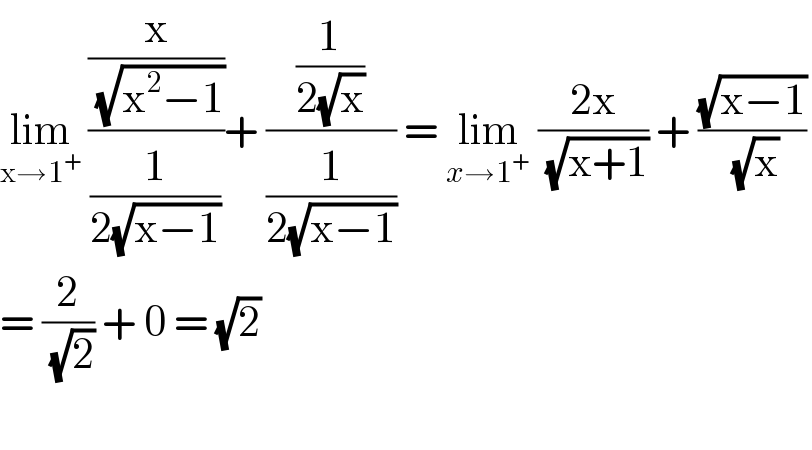
$$\underset{\mathrm{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\:\frac{\frac{\mathrm{x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}}{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}−\mathrm{1}}}}+\:\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}}{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}−\mathrm{1}}}}\:=\:\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\:\frac{\mathrm{2x}}{\:\sqrt{\mathrm{x}+\mathrm{1}}}\:+\:\frac{\sqrt{\mathrm{x}−\mathrm{1}}}{\:\sqrt{\mathrm{x}}} \\ $$$$=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}\:+\:\mathrm{0}\:=\:\sqrt{\mathrm{2}}\: \\ $$$$ \\ $$
Commented by john santu last updated on 24/Jun/20
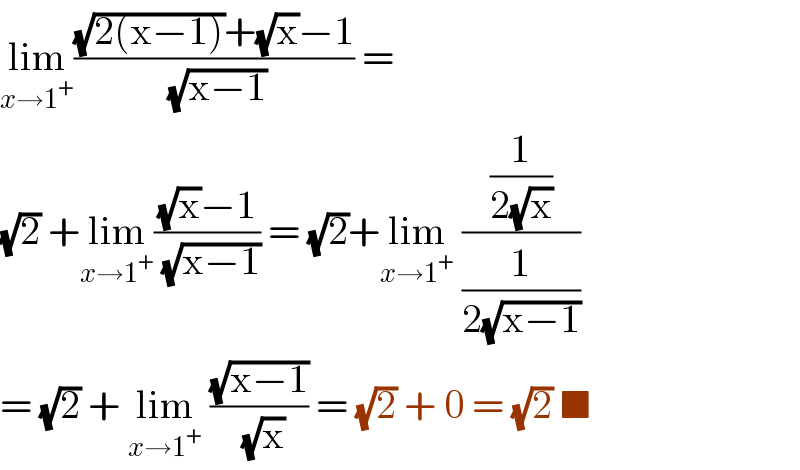
$$\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\frac{\sqrt{\mathrm{2}\left(\mathrm{x}−\mathrm{1}\right)}+\sqrt{\mathrm{x}}−\mathrm{1}}{\:\sqrt{\mathrm{x}−\mathrm{1}}}\:= \\ $$$$\sqrt{\mathrm{2}}\:+\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\frac{\sqrt{\mathrm{x}}−\mathrm{1}}{\:\sqrt{\mathrm{x}−\mathrm{1}}}\:=\:\sqrt{\mathrm{2}}+\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}}{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}−\mathrm{1}}}} \\ $$$$=\:\sqrt{\mathrm{2}}\:+\:\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\:\frac{\sqrt{\mathrm{x}−\mathrm{1}}}{\:\sqrt{\mathrm{x}}}\:=\:\sqrt{\mathrm{2}}\:+\:\mathrm{0}\:=\:\sqrt{\mathrm{2}}\:\blacksquare \\ $$
Answered by mathmax by abdo last updated on 24/Jun/20

$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}+\sqrt{\mathrm{x}}−\mathrm{1}}{\:\sqrt{\mathrm{x}−\mathrm{1}}}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{thechangement}\:\sqrt{\mathrm{x}−\mathrm{1}}=\mathrm{t}\:\Rightarrow\mathrm{x}−\mathrm{1}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\sqrt{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}+\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }−\mathrm{1}}{\mathrm{t}}\:=\frac{\sqrt{\mathrm{t}^{\mathrm{4}} +\mathrm{2t}^{\mathrm{2}} }+\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }−\mathrm{1}}{\mathrm{t}}=\mathrm{g}\left(\mathrm{t}\right) \\ $$$$\mathrm{x}\rightarrow\mathrm{1}^{+} \:\Rightarrow\mathrm{t}\rightarrow\mathrm{0}^{+} \:\Rightarrow\:\mathrm{g}\left(\mathrm{t}\right)\:=\frac{\mathrm{t}\sqrt{\mathrm{2}}\sqrt{\mathrm{1}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}}+\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }−\mathrm{1}}{\mathrm{t}} \\ $$$$\Rightarrow\mathrm{g}\left(\mathrm{t}\right)\:\sim\frac{\mathrm{t}\sqrt{\mathrm{2}}\left\{\mathrm{1}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{4}}\right\}+\mathrm{1}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}}{\mathrm{t}}\:=\sqrt{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{4}}\right)+\frac{\mathrm{t}}{\mathrm{2}}\:\Rightarrow\sqrt{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}^{+} } \:\:\:\mathrm{g}\left(\mathrm{x}\right)\:=\sqrt{\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 24/Jun/20
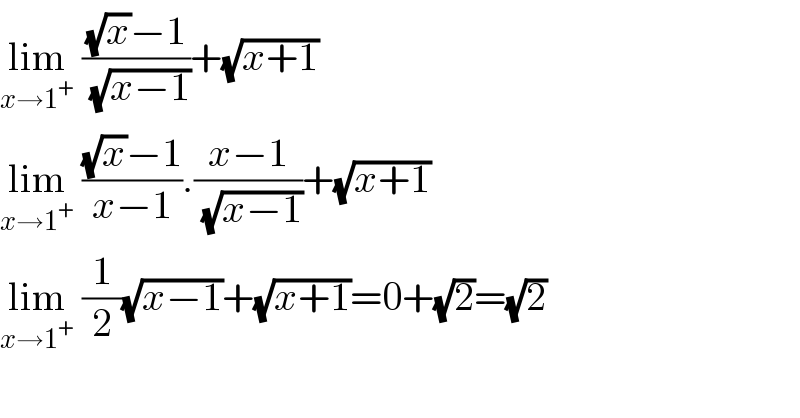
$$\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\:\frac{\sqrt{{x}}−\mathrm{1}}{\:\sqrt{{x}−\mathrm{1}}}+\sqrt{{x}+\mathrm{1}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\:\frac{\sqrt{{x}}−\mathrm{1}}{{x}−\mathrm{1}}.\frac{{x}−\mathrm{1}}{\:\sqrt{{x}−\mathrm{1}}}+\sqrt{{x}+\mathrm{1}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{x}−\mathrm{1}}+\sqrt{{x}+\mathrm{1}}=\mathrm{0}+\sqrt{\mathrm{2}}=\sqrt{\mathrm{2}} \\ $$$$ \\ $$
