Question Number 161560 by lapache last updated on 19/Dec/21
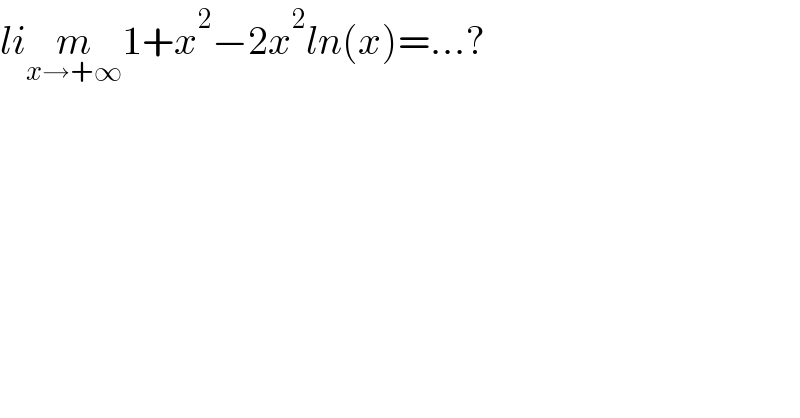
$${li}\underset{{x}\rightarrow+\infty} {{m}}\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} {ln}\left({x}\right)=…? \\ $$
Answered by mathmax by abdo last updated on 19/Dec/21
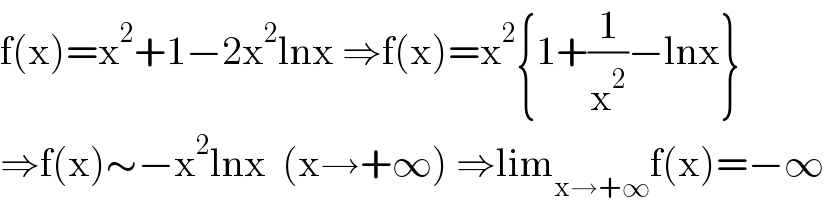
$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2x}^{\mathrm{2}} \mathrm{lnx}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} \left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{lnx}\right\} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim−\mathrm{x}^{\mathrm{2}} \mathrm{lnx}\:\:\left(\mathrm{x}\rightarrow+\infty\right)\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)=−\infty \\ $$
