Question Number 118327 by bramlexs22 last updated on 17/Oct/20
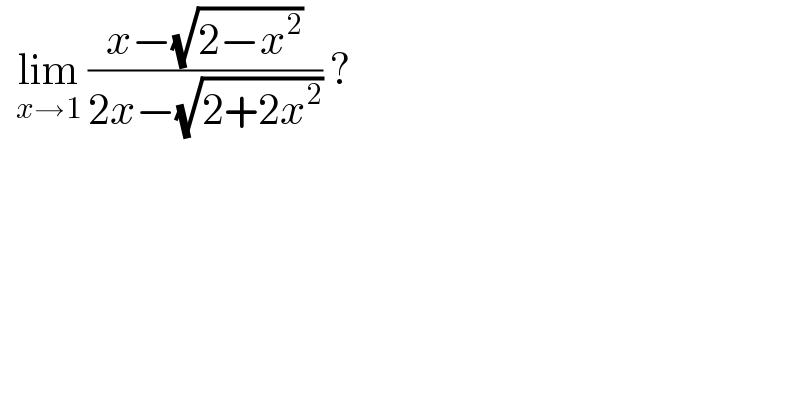
$$\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}−\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}{\mathrm{2}{x}−\sqrt{\mathrm{2}+\mathrm{2}{x}^{\mathrm{2}} }}\:? \\ $$
Answered by TANMAY PANACEA last updated on 17/Oct/20
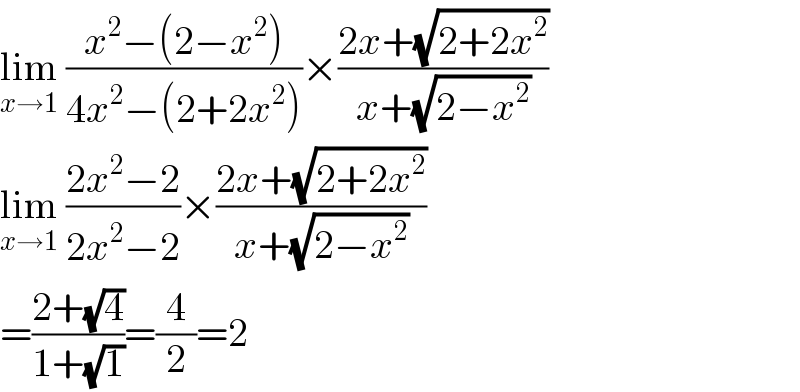
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} −\left(\mathrm{2}−{x}^{\mathrm{2}} \right)}{\mathrm{4}{x}^{\mathrm{2}} −\left(\mathrm{2}+\mathrm{2}{x}^{\mathrm{2}} \right)}×\frac{\mathrm{2}{x}+\sqrt{\mathrm{2}+\mathrm{2}{x}^{\mathrm{2}} }}{{x}+\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}}×\frac{\mathrm{2}{x}+\sqrt{\mathrm{2}+\mathrm{2}{x}^{\mathrm{2}} }}{{x}+\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{2}+\sqrt{\mathrm{4}}}{\mathrm{1}+\sqrt{\mathrm{1}}}=\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{2} \\ $$
Answered by bramlexs22 last updated on 17/Oct/20
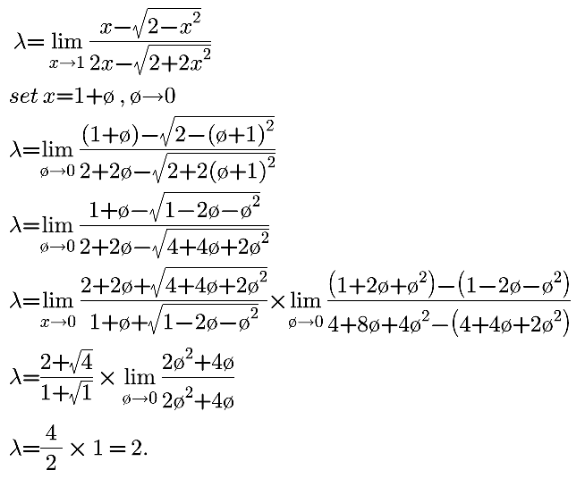
Answered by benjo_mathlover last updated on 17/Oct/20
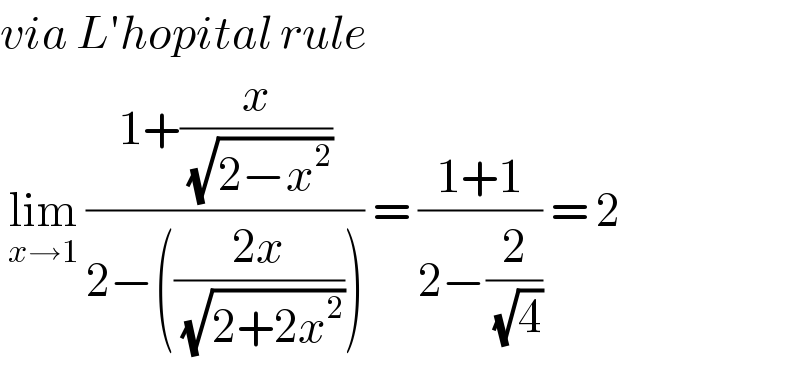
$${via}\:{L}'{hopital}\:{rule}\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}+\frac{{x}}{\:\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}}{\mathrm{2}−\left(\frac{\mathrm{2}{x}}{\:\sqrt{\mathrm{2}+\mathrm{2}{x}^{\mathrm{2}} }}\right)}\:=\:\frac{\mathrm{1}+\mathrm{1}}{\mathrm{2}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}}}}\:=\:\mathrm{2} \\ $$
Answered by 1549442205PVT last updated on 17/Oct/20
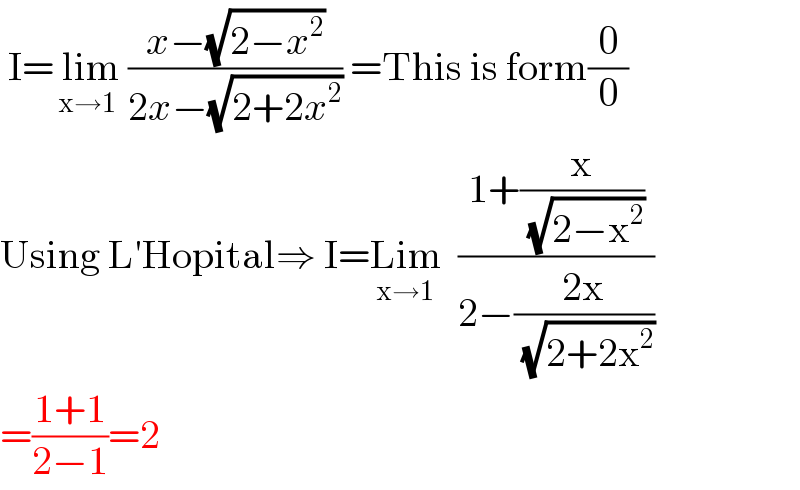
$$\:\mathrm{I}=\underset{\mathrm{x}\rightarrow\mathrm{1}} {\:\mathrm{lim}}\:\frac{{x}−\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}{\mathrm{2}{x}−\sqrt{\mathrm{2}+\mathrm{2}{x}^{\mathrm{2}} }}\:=\mathrm{This}\:\mathrm{is}\:\mathrm{form}\frac{\mathrm{0}}{\mathrm{0}}\: \\ $$$$\mathrm{Using}\:\mathrm{L}'\mathrm{Hopital}\Rightarrow\:\mathrm{I}=\underset{\mathrm{x}\rightarrow\mathrm{1}} {\mathrm{Lim}}\:\:\frac{\mathrm{1}+\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }}}{\mathrm{2}−\frac{\mathrm{2x}}{\:\sqrt{\mathrm{2}+\mathrm{2x}^{\mathrm{2}} }}} \\ $$$$=\frac{\mathrm{1}+\mathrm{1}}{\mathrm{2}−\mathrm{1}}=\mathrm{2} \\ $$
