Question Number 27723 by NECx last updated on 13/Jan/18
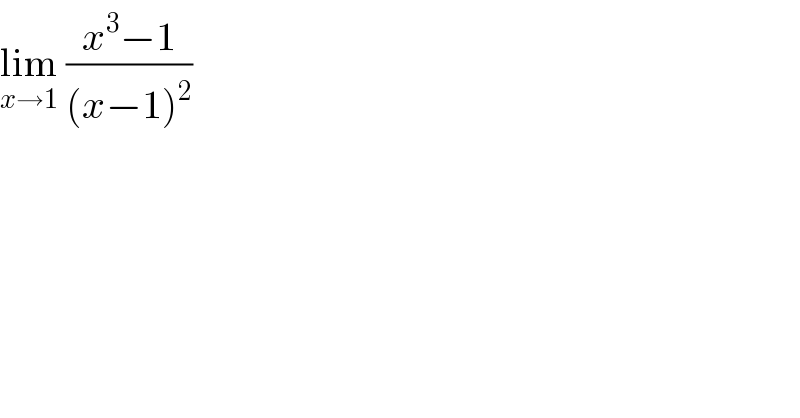
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} −\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Answered by prakash jain last updated on 13/Jan/18
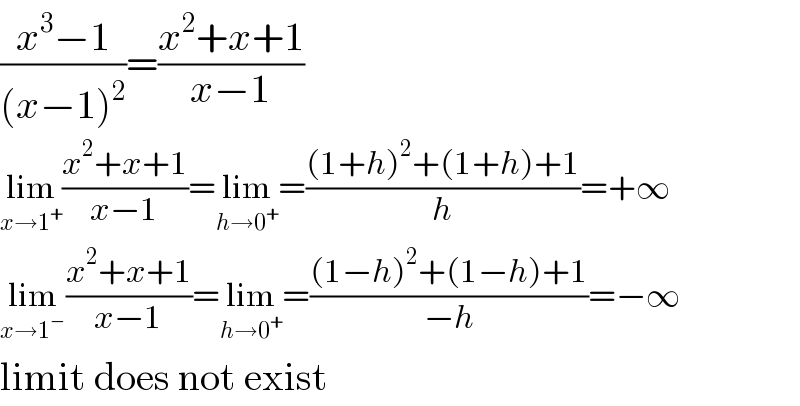
$$\frac{{x}^{\mathrm{3}} −\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }=\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{{x}−\mathrm{1}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{{x}−\mathrm{1}}=\underset{{h}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}=\frac{\left(\mathrm{1}+{h}\right)^{\mathrm{2}} +\left(\mathrm{1}+{h}\right)+\mathrm{1}}{{h}}=+\infty \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{{x}−\mathrm{1}}=\underset{{h}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}=\frac{\left(\mathrm{1}−{h}\right)^{\mathrm{2}} +\left(\mathrm{1}−{h}\right)+\mathrm{1}}{−{h}}=−\infty \\ $$$$\mathrm{limit}\:\mathrm{does}\:\mathrm{not}\:\mathrm{exist} \\ $$
Commented by NECx last updated on 13/Jan/18

$${thanks} \\ $$
