Question Number 62067 by naka3546 last updated on 15/Jun/19
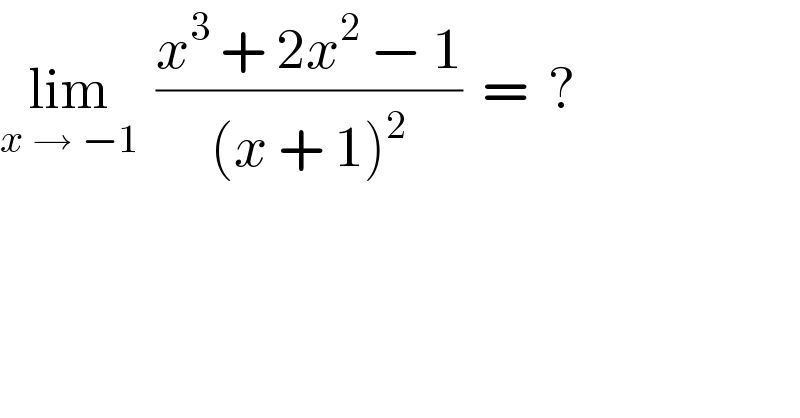
$$\underset{{x}\:\rightarrow\:−\mathrm{1}} {\mathrm{lim}}\:\:\frac{{x}^{\mathrm{3}} \:+\:\mathrm{2}{x}^{\mathrm{2}} \:−\:\mathrm{1}}{\left({x}\:+\:\mathrm{1}\right)^{\mathrm{2}} }\:\:=\:\:? \\ $$
Commented by gunawan last updated on 15/Jun/19
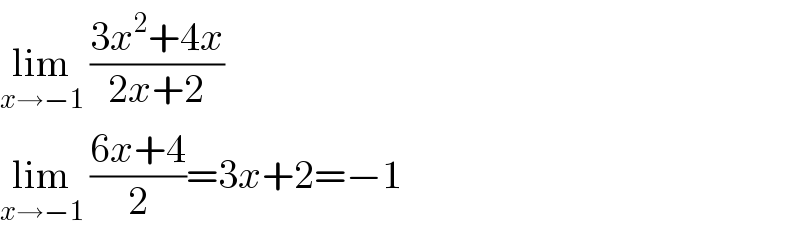
$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}}{\mathrm{2}{x}+\mathrm{2}} \\ $$$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{6}{x}+\mathrm{4}}{\mathrm{2}}=\mathrm{3}{x}+\mathrm{2}=−\mathrm{1} \\ $$
Commented by Tony Lin last updated on 15/Jun/19
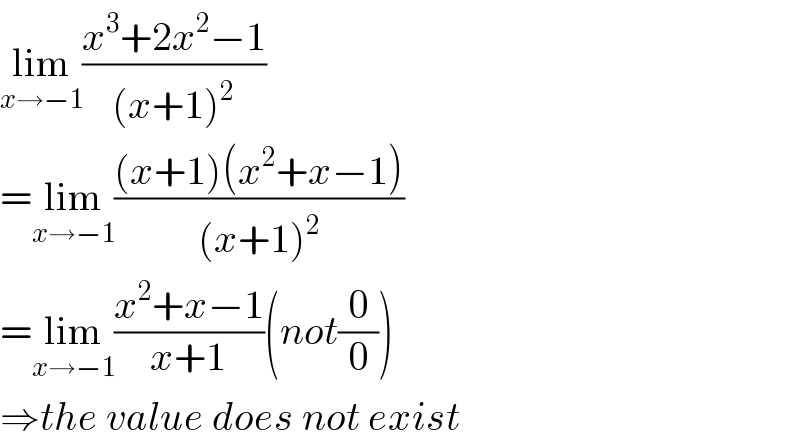
$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}−\mathrm{1}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} +{x}−\mathrm{1}}{{x}+\mathrm{1}}\left({not}\frac{\mathrm{0}}{\mathrm{0}}\right) \\ $$$$\Rightarrow{the}\:{value}\:{does}\:{not}\:{exist} \\ $$
Commented by Tony Lin last updated on 15/Jun/19
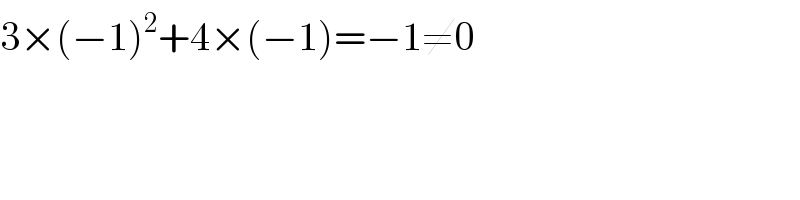
$$\mathrm{3}×\left(−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}×\left(−\mathrm{1}\right)=−\mathrm{1}\neq\mathrm{0} \\ $$
Answered by MIR ZAKIR last updated on 15/Jun/19

$${lim} \\ $$$${x}−\phi \\ $$
Answered by MJS last updated on 15/Jun/19
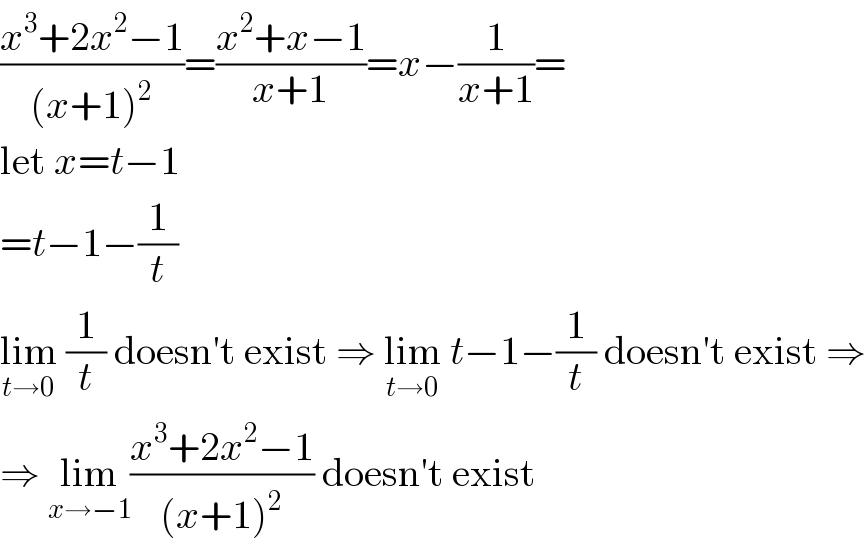
$$\frac{{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{{x}^{\mathrm{2}} +{x}−\mathrm{1}}{{x}+\mathrm{1}}={x}−\frac{\mathrm{1}}{{x}+\mathrm{1}}= \\ $$$$\mathrm{let}\:{x}={t}−\mathrm{1} \\ $$$$={t}−\mathrm{1}−\frac{\mathrm{1}}{{t}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{t}}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist}\:\Rightarrow\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{t}−\mathrm{1}−\frac{\mathrm{1}}{{t}}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist}\:\Rightarrow \\ $$$$\Rightarrow\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist} \\ $$
