Question Number 186065 by TUN last updated on 31/Jan/23
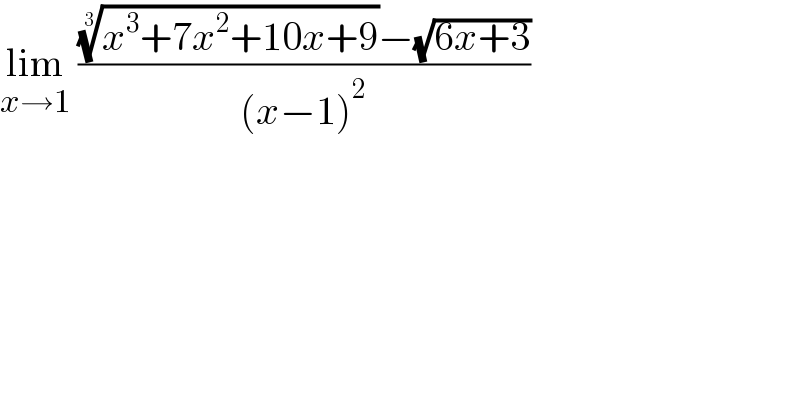
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +\mathrm{7}{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{9}}−\sqrt{\mathrm{6}{x}+\mathrm{3}}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$ \\ $$
Commented by Frix last updated on 01/Feb/23
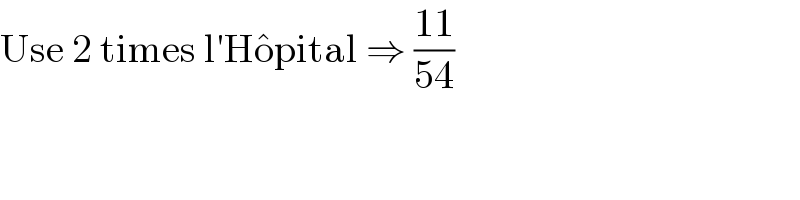
$$\mathrm{Use}\:\mathrm{2}\:\mathrm{times}\:\mathrm{l}'\mathrm{H}\hat {\mathrm{o}pital}\:\Rightarrow\:\frac{\mathrm{11}}{\mathrm{54}} \\ $$
Commented by TUN last updated on 01/Feb/23
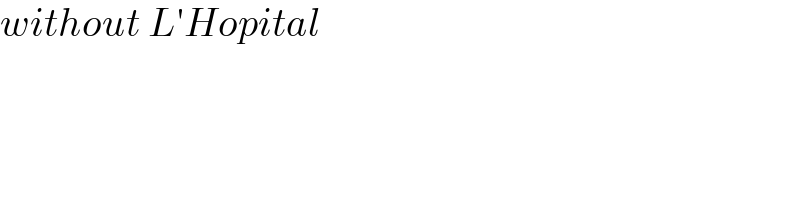
$${without}\:{L}'{Hopital} \\ $$
Answered by cortano1 last updated on 01/Feb/23
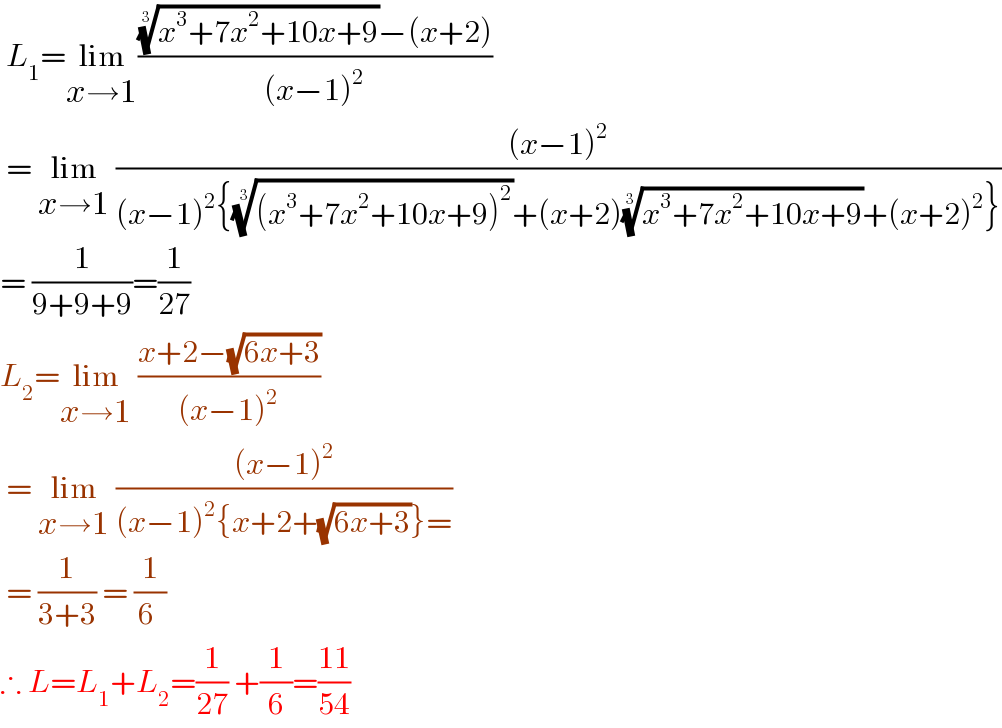
$$\:{L}_{\mathrm{1}} =\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +\mathrm{7}{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{9}}−\left({x}+\mathrm{2}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left\{\sqrt[{\mathrm{3}}]{\left({x}^{\mathrm{3}} +\mathrm{7}{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{9}\right)^{\mathrm{2}} }+\left({x}+\mathrm{2}\right)\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +\mathrm{7}{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{9}}+\left({x}+\mathrm{2}\right)^{\mathrm{2}} \right\}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{9}+\mathrm{9}+\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{27}} \\ $$$${L}_{\mathrm{2}} =\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}+\mathrm{2}−\sqrt{\mathrm{6}{x}+\mathrm{3}}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left\{{x}+\mathrm{2}+\sqrt{\mathrm{6}{x}+\mathrm{3}}\right\}=} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{3}+\mathrm{3}}\:=\:\frac{\mathrm{1}}{\mathrm{6}\:} \\ $$$$\therefore\:{L}={L}_{\mathrm{1}} +{L}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{27}}\:+\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{11}}{\mathrm{54}} \\ $$
