lim-x-1-x-4-1-4-1-x-5-1-5-

Question Number 118247 by bemath last updated on 16/Oct/20

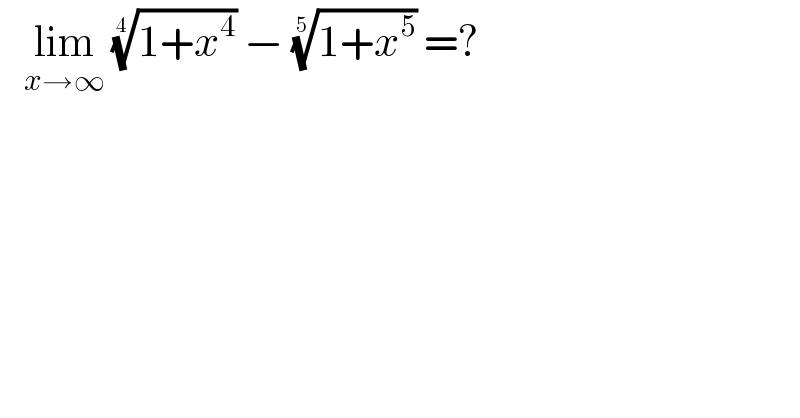
$$\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{4}}]{\mathrm{1}+{x}^{\mathrm{4}} }\:−\:\sqrt[{\mathrm{5}}]{\mathrm{1}+{x}^{\mathrm{5}} }\:=? \\ $$

Answered by bobhans last updated on 16/Oct/20

solve lim_(x→∞) ((1+x^4 ))^(1/4) − ((1+x^5 ))^(1/(5 )) . solution: let x = (1/z) ; z→0 lim_(z→0) ((1+(1/z^4 )))^(1/4) −((1+(1/z^5 ) ))^(1/5) = lim_(z→0) ((((z^4 +1))^(1/4) −((z^5 +1))^(1/5) )/z) = lim_(z→0) ((((z^4 /4)+1)−((z^5 /5)+1))/z) = lim_(z→0) ((((z^4 /4) −(z^5 /5))/z) ) lim_(z→0) (z^3 /4) − (z^4 /5) = 0

$${solve}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{4}}]{\mathrm{1}+{x}^{\mathrm{4}} }\:−\:\sqrt[{\mathrm{5}\:}]{\mathrm{1}+{x}^{\mathrm{5}} }\:. \\ $$$${solution}:\: \\ $$$${let}\:{x}\:=\:\frac{\mathrm{1}}{{z}}\:;\:{z}\rightarrow\mathrm{0} \\ $$$$\:\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt[{\mathrm{4}}]{\mathrm{1}+\frac{\mathrm{1}}{{z}^{\mathrm{4}} }}−\sqrt[{\mathrm{5}}]{\mathrm{1}+\frac{\mathrm{1}}{{z}^{\mathrm{5}} }\:}\:=\: \\ $$$$\:\:\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{4}}]{{z}^{\mathrm{4}} +\mathrm{1}}−\sqrt[{\mathrm{5}}]{{z}^{\mathrm{5}} +\mathrm{1}}}{{z}}\:=\: \\ $$$$\:\:\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\frac{{z}^{\mathrm{4}} }{\mathrm{4}}+\mathrm{1}\right)−\left(\frac{{z}^{\mathrm{5}} }{\mathrm{5}}+\mathrm{1}\right)}{{z}}\:=\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\frac{{z}^{\mathrm{4}} }{\mathrm{4}}\:−\frac{{z}^{\mathrm{5}} }{\mathrm{5}}}{{z}}\:\right)\:\: \\ $$$$\:\:\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{z}^{\mathrm{3}} }{\mathrm{4}}\:−\:\frac{{z}^{\mathrm{4}} }{\mathrm{5}}\:=\:\mathrm{0} \\ $$$$ \\ $$

Commented by bemath last updated on 16/Oct/20

$${gave}\:{kudos}\:{man}\: \\ $$

Answered by mathmax by abdo last updated on 16/Oct/20

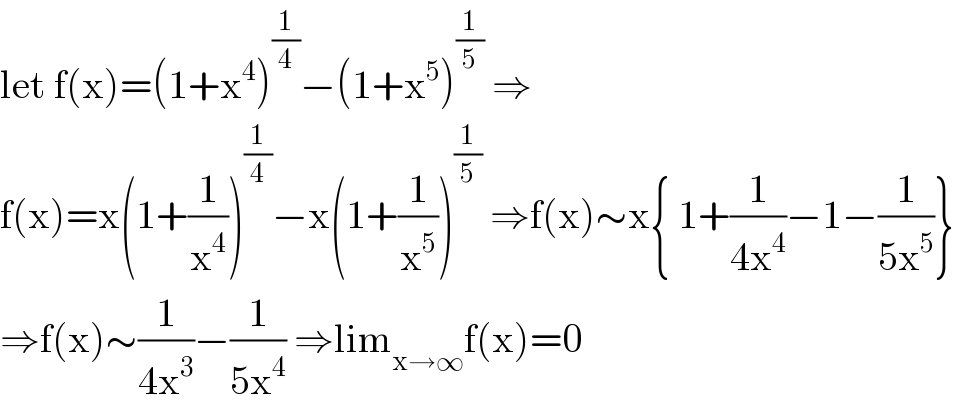
let f(x)=(1+x^4 )^(1/4) −(1+x^5 )^(1/5) ⇒ f(x)=x(1+(1/x^4 ))^(1/4) −x(1+(1/x^5 ))^(1/5) ⇒f(x)∼x{ 1+(1/(4x^4 ))−1−(1/(5x^5 ))} ⇒f(x)∼(1/(4x^3 ))−(1/(5x^4 )) ⇒lim_(x→∞) f(x)=0

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} −\left(\mathrm{1}+\mathrm{x}^{\mathrm{5}} \right)^{\frac{\mathrm{1}}{\mathrm{5}}} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }\right)^{\frac{\mathrm{1}}{\mathrm{4}}} −\mathrm{x}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{5}} }\right)^{\frac{\mathrm{1}}{\mathrm{5}}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\mathrm{x}\left\{\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4x}^{\mathrm{4}} }−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5x}^{\mathrm{5}} }\right\} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{1}}{\mathrm{4x}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{5x}^{\mathrm{4}} }\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{0} \\ $$

Facebook Tweet Pin

lim-x-1-x-4-1-4-1-x-5-1-5-

Leave a Reply Cancel reply