Question Number 109139 by bemath last updated on 21/Aug/20
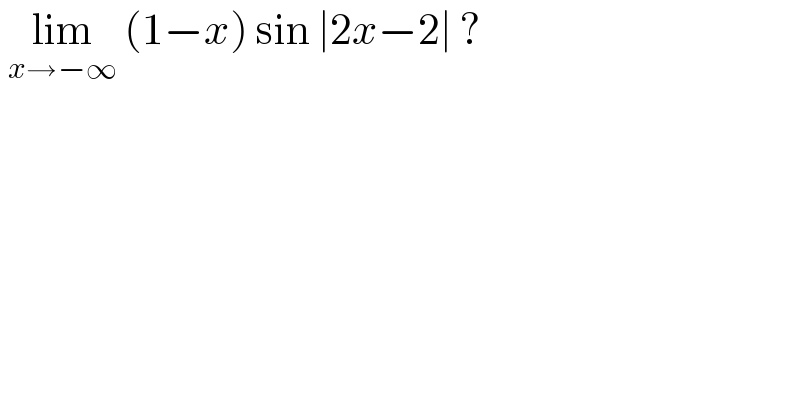
$$\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\left(\mathrm{1}−{x}\right)\:\mathrm{sin}\:\mid\mathrm{2}{x}−\mathrm{2}\mid\:? \\ $$
Commented by kaivan.ahmadi last updated on 21/Aug/20
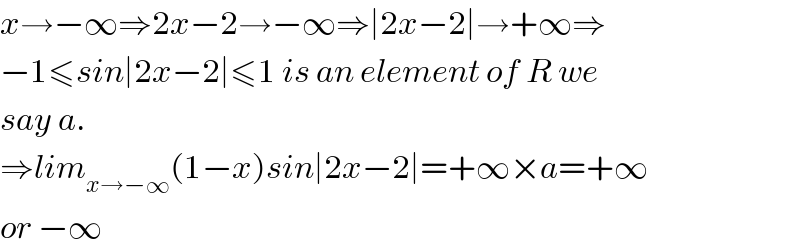
$${x}\rightarrow−\infty\Rightarrow\mathrm{2}{x}−\mathrm{2}\rightarrow−\infty\Rightarrow\mid\mathrm{2}{x}−\mathrm{2}\mid\rightarrow+\infty\Rightarrow \\ $$$$−\mathrm{1}\leqslant{sin}\mid\mathrm{2}{x}−\mathrm{2}\mid\leqslant\mathrm{1}\:{is}\:{an}\:{element}\:{of}\:{R}\:{we} \\ $$$${say}\:{a}. \\ $$$$\Rightarrow{lim}_{{x}\rightarrow−\infty} \left(\mathrm{1}−{x}\right){sin}\mid\mathrm{2}{x}−\mathrm{2}\mid=+\infty×{a}=+\infty \\ $$$${or}\:−\infty \\ $$
