Question Number 128605 by john_santu last updated on 08/Jan/21
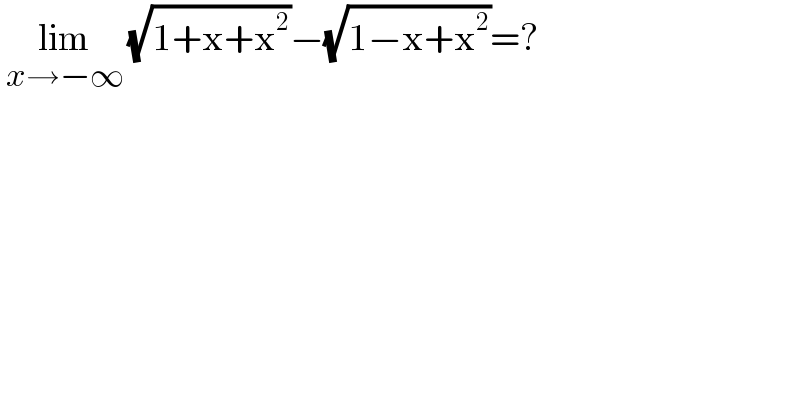
$$\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\sqrt{\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} }−\sqrt{\mathrm{1}−\mathrm{x}+\mathrm{x}^{\mathrm{2}} }=? \\ $$
Commented by john_santu last updated on 08/Jan/21
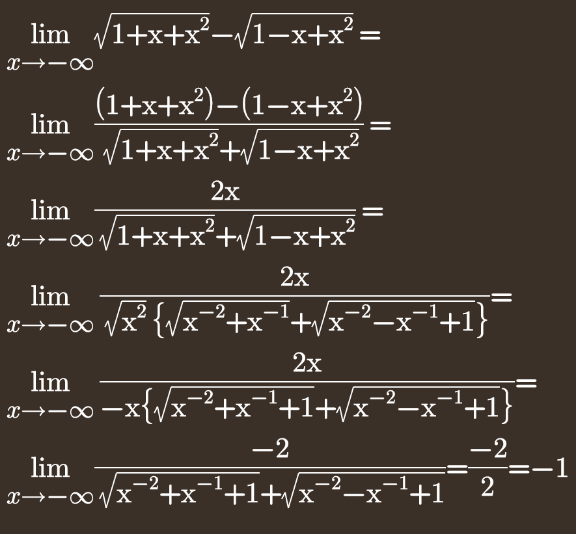
Answered by mathmax by abdo last updated on 09/Jan/21
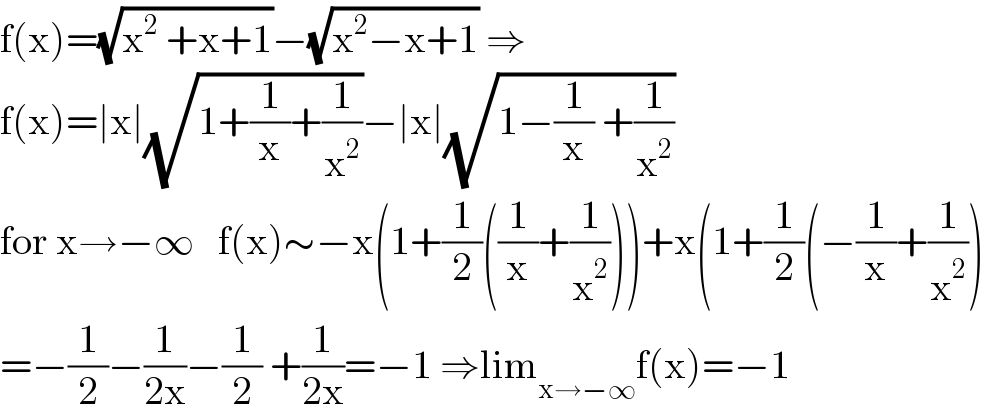
$$\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}}−\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mid\mathrm{x}\mid\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}−\mid\mathrm{x}\mid\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}\:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{for}\:\mathrm{x}\rightarrow−\infty\:\:\:\mathrm{f}\left(\mathrm{x}\right)\sim−\mathrm{x}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\right)+\mathrm{x}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\right. \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2x}}−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2x}}=−\mathrm{1}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} \mathrm{f}\left(\mathrm{x}\right)=−\mathrm{1} \\ $$
