Question Number 156788 by mathlove last updated on 15/Oct/21
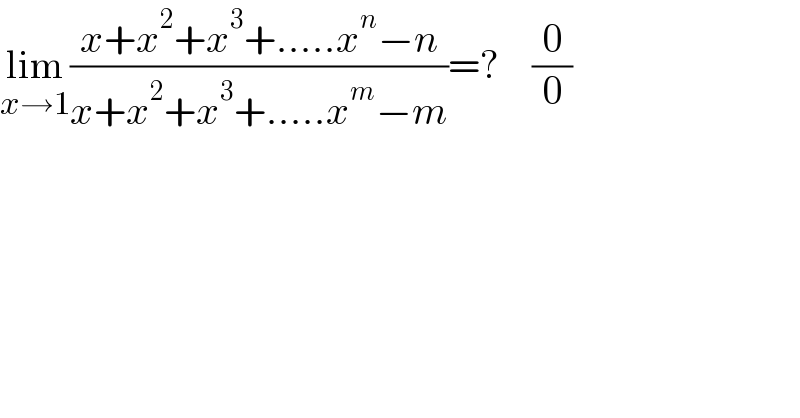
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…..{x}^{{n}} −{n}}{{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…..{x}^{{m}} −{m}}=?\:\:\:\:\frac{\mathrm{0}}{\mathrm{0}} \\ $$
Answered by puissant last updated on 15/Oct/21
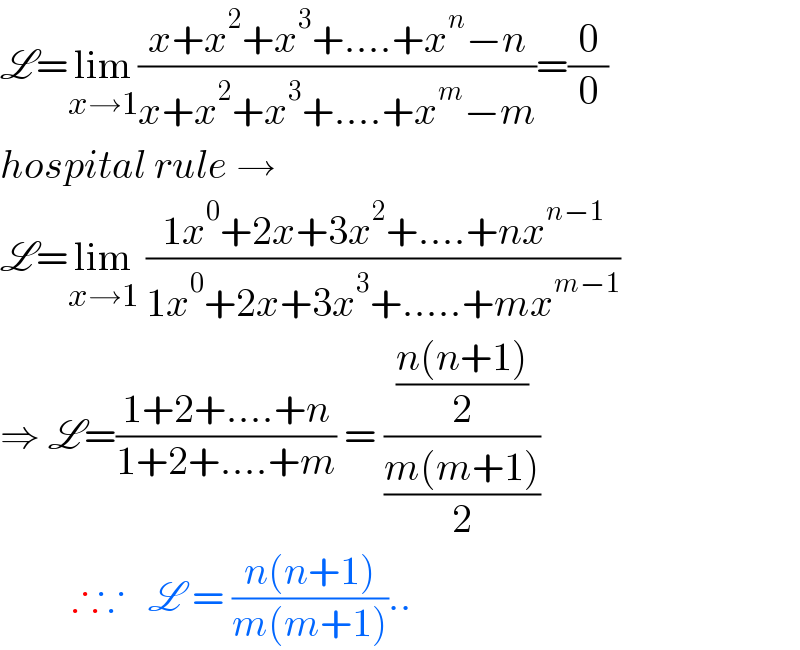
$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +….+{x}^{{n}} −{n}}{{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +….+{x}^{{m}} −{m}}=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$${hospital}\:{rule}\:\rightarrow\: \\ $$$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}{x}^{\mathrm{0}} +\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +….+{nx}^{{n}−\mathrm{1}} }{\mathrm{1}{x}^{\mathrm{0}} +\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{3}} +…..+{mx}^{{m}−\mathrm{1}} } \\ $$$$\Rightarrow\:\mathscr{L}=\frac{\mathrm{1}+\mathrm{2}+….+{n}}{\mathrm{1}+\mathrm{2}+….+{m}}\:=\:\frac{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}}{\frac{{m}\left({m}+\mathrm{1}\right)}{\mathrm{2}}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\therefore\because\:\:\:\mathscr{L}\:=\:\frac{{n}\left({n}+\mathrm{1}\right)}{{m}\left({m}+\mathrm{1}\right)}.. \\ $$
Commented by mathlove last updated on 15/Oct/21
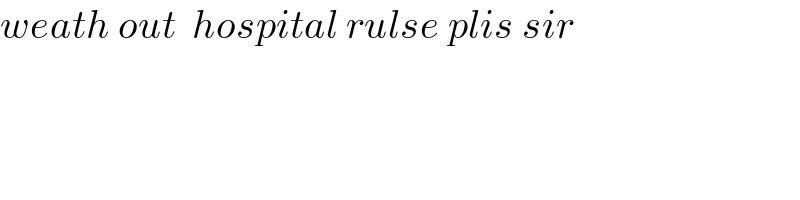
$${weath}\:{out}\:\:{hospital}\:{rulse}\:{plis}\:{sir} \\ $$
Commented by puissant last updated on 15/Oct/21
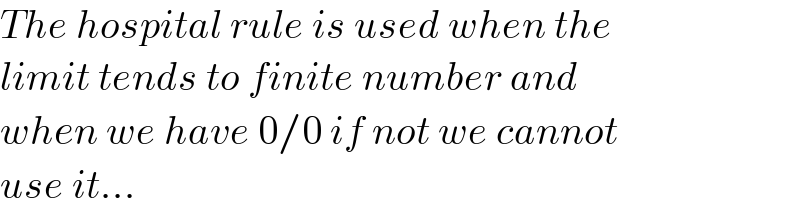
$${The}\:{hospital}\:{rule}\:{is}\:{used}\:{when}\:{the}\: \\ $$$${limit}\:{tends}\:{to}\:{finite}\:{number}\:{and}\: \\ $$$${when}\:{we}\:{have}\:\mathrm{0}/\mathrm{0}\:{if}\:{not}\:{we}\:{cannot} \\ $$$${use}\:{it}… \\ $$
Answered by FongXD last updated on 15/Oct/21
![Without L′hospital′s rule =lim_(x→1) (((x−1)+(x^2 −1)+(x^3 −1)+...+(x^n −1))/((x−1)+(x^2 −1)+(x^3 −1)+...+(x^m −1))) =lim_(x→1) (((x−1)[1+(x+1)+(x^2 +x+1)+...+(x^(n−1) +x^(n−2) +...+x+1)])/((x−1)[1+(x+1)+(x^2 +x+1)+...+(x^(m−1) +x^(m−2) +...+x+1)])) =lim_(x→1) ((1+(x+1)+(x^2 +x+1)+...+(x^(n−1) +x^(n−2) +...+x+1))/(1+(x+1)+(x^2 +x+1)+...+(x^(m−1) +x^(m−2) +...+x+1))) =((1+2+3+...+n)/(1+2+3+...+m))=(((n(n+1))/2)/((m(m+1))/2))=((n(n+1))/(m(m+1)))](https://www.tinkutara.com/question/Q156803.png)
$$\mathrm{Without}\:\mathrm{L}'\mathrm{hospital}'\mathrm{s}\:\mathrm{rule} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left(\mathrm{x}−\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)+…+\left(\mathrm{x}^{\mathrm{n}} −\mathrm{1}\right)}{\left(\mathrm{x}−\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)+…+\left(\mathrm{x}^{\mathrm{m}} −\mathrm{1}\right)} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left(\mathrm{x}−\mathrm{1}\right)\left[\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)+…+\left(\mathrm{x}^{\mathrm{n}−\mathrm{1}} +\mathrm{x}^{\mathrm{n}−\mathrm{2}} +…+\mathrm{x}+\mathrm{1}\right)\right]}{\left(\mathrm{x}−\mathrm{1}\right)\left[\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)+…+\left(\mathrm{x}^{\mathrm{m}−\mathrm{1}} +\mathrm{x}^{\mathrm{m}−\mathrm{2}} +…+\mathrm{x}+\mathrm{1}\right)\right]} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)+…+\left(\mathrm{x}^{\mathrm{n}−\mathrm{1}} +\mathrm{x}^{\mathrm{n}−\mathrm{2}} +…+\mathrm{x}+\mathrm{1}\right)}{\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)+…+\left(\mathrm{x}^{\mathrm{m}−\mathrm{1}} +\mathrm{x}^{\mathrm{m}−\mathrm{2}} +…+\mathrm{x}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}+\mathrm{2}+\mathrm{3}+…+\mathrm{n}}{\mathrm{1}+\mathrm{2}+\mathrm{3}+…+\mathrm{m}}=\frac{\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}}{\frac{\mathrm{m}\left(\mathrm{m}+\mathrm{1}\right)}{\mathrm{2}}}=\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{m}\left(\mathrm{m}+\mathrm{1}\right)} \\ $$
Commented by mathlove last updated on 16/Oct/21

$${thanks}\:{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 16/Oct/21

$$\mathcal{N}{ice}\:\mathcal{S}{ir}! \\ $$
Answered by mindispower last updated on 16/Oct/21
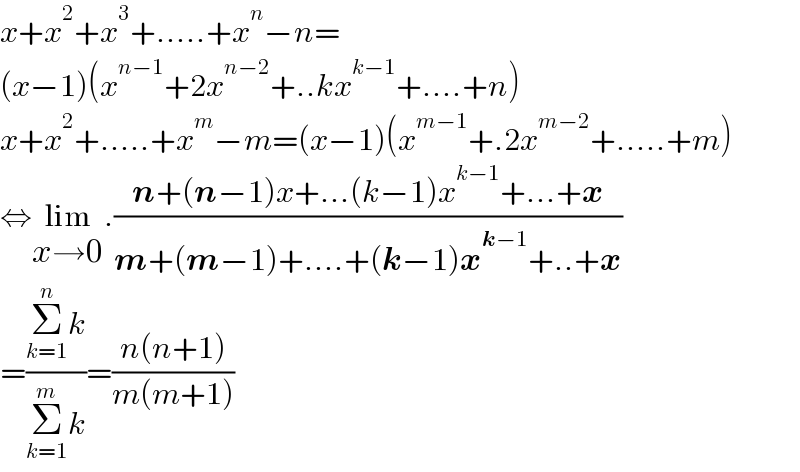
$${x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…..+{x}^{{n}} −{n}= \\ $$$$\left({x}−\mathrm{1}\right)\left({x}^{{n}−\mathrm{1}} +\mathrm{2}{x}^{{n}−\mathrm{2}} +..{kx}^{{k}−\mathrm{1}} +….+{n}\right) \\ $$$${x}+{x}^{\mathrm{2}} +…..+{x}^{{m}} −{m}=\left({x}−\mathrm{1}\right)\left({x}^{{m}−\mathrm{1}} +.\mathrm{2}{x}^{{m}−\mathrm{2}} +…..+{m}\right) \\ $$$$\Leftrightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}.\frac{\boldsymbol{{n}}+\left(\boldsymbol{{n}}−\mathrm{1}\right){x}+…\left({k}−\mathrm{1}\right){x}^{{k}−\mathrm{1}} +…+\boldsymbol{{x}}}{\boldsymbol{{m}}+\left(\boldsymbol{{m}}−\mathrm{1}\right)+….+\left(\boldsymbol{{k}}−\mathrm{1}\right)\boldsymbol{{x}}^{\boldsymbol{{k}}−\mathrm{1}} +..+\boldsymbol{{x}}} \\ $$$$=\frac{\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}}{\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}{k}}=\frac{{n}\left({n}+\mathrm{1}\right)}{{m}\left({m}+\mathrm{1}\right)} \\ $$
