Menu Close

lim-x-2-1-sin-pi-x-x-2-4x-4-lim-x-2-x-3-8-sin-pix-2-x-lim-x-1-x-2-1-cos-pi-x-1-

Tinku Tara 0 Comments
Pin




Question Number 161583 by cortano last updated on 19/Dec/21
lim_(x→2) ((1−sin (π/x))/(x^2 −4x+4)) =? lim_(x→2) ((x^3 −8+sin πx)/(2−x))=? lim_(x→1) ((x^2 −1)/(cos ((π/(x+1)))))=?
$$\:\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{sin}\:\frac{\pi}{{x}}}{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}}\:=? \\ $$$$\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} −\mathrm{8}+\mathrm{sin}\:\pi{x}}{\mathrm{2}−{x}}=? \\ $$$$\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{cos}\:\left(\frac{\pi}{{x}+\mathrm{1}}\right)}=? \\ $$
Commented by blackmamba last updated on 20/Dec/21
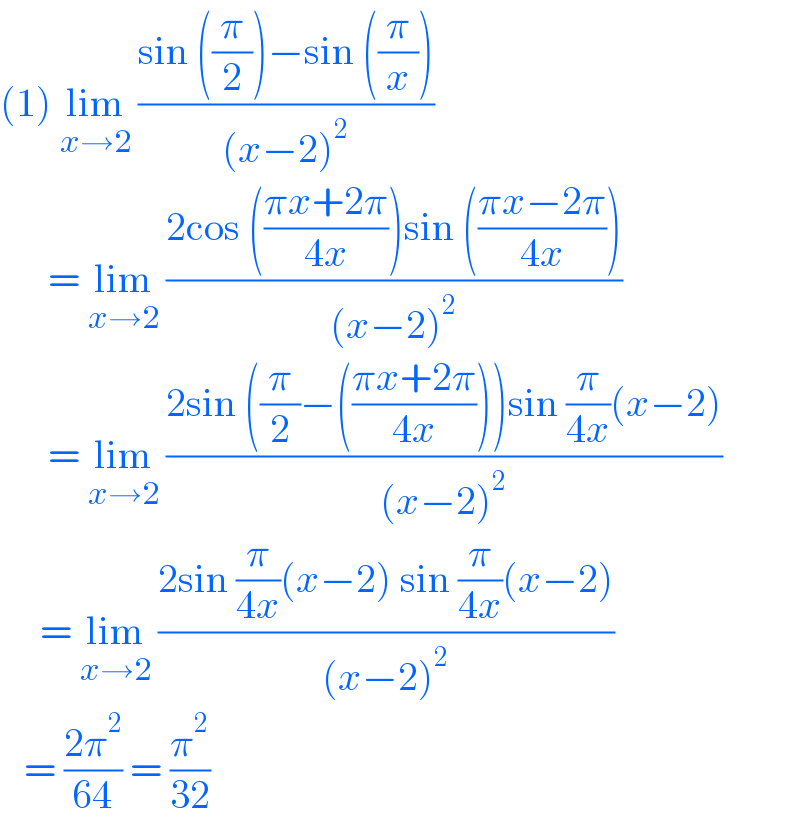
(1) lim_(x→2) ((sin ((π/2))−sin ((π/x)))/((x−2)^2 )) = lim_(x→2) ((2cos (((πx+2π)/(4x)))sin (((πx−2π)/(4x))))/((x−2)^2 )) = lim_(x→2) ((2sin ((π/2)−(((πx+2π)/(4x))))sin (π/(4x))(x−2))/((x−2)^2 )) = lim_(x→2) ((2sin (π/(4x))(x−2) sin (π/(4x))(x−2))/((x−2)^2 )) = ((2π^2 )/(64)) = (π^2 /(32))
$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}\right)−\mathrm{sin}\:\left(\frac{\pi}{{x}}\right)}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{2cos}\:\left(\frac{\pi{x}+\mathrm{2}\pi}{\mathrm{4}{x}}\right)\mathrm{sin}\:\left(\frac{\pi{x}−\mathrm{2}\pi}{\mathrm{4}{x}}\right)}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{2sin}\:\left(\frac{\pi}{\mathrm{2}}−\left(\frac{\pi{x}+\mathrm{2}\pi}{\mathrm{4}{x}}\right)\right)\mathrm{sin}\:\frac{\pi}{\mathrm{4}{x}}\left({x}−\mathrm{2}\right)}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{2sin}\:\frac{\pi}{\mathrm{4}{x}}\left({x}−\mathrm{2}\right)\:\mathrm{sin}\:\frac{\pi}{\mathrm{4}{x}}\left({x}−\mathrm{2}\right)}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\:\:\:=\:\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{64}}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{32}} \\ $$
Answered by Ar Brandon last updated on 20/Dec/21
lim_(x→1) ((x^2 −1)/(cos((π/(x+1)))))=lim_(x→1) (((x+1)(x−1))/(cos((π/(x+1)))))=lim_(x→1) (((x+1)(x−1))/(sin((π/2)−(π/(x+1))))) lim_(x→1) (((x+1)(x−1))/(sin(((π(x−1))/(2(x+1))))))=lim_(x→1) ((2(x+1)^2 )/π)∙(((π/2)(((x−1)/(x+1))))/(sin((π/2)(((x−1)/(x+1)))))) =lim_(x→1) ((2(x+1)^2 )/π)∙lim_(x→1) ((((π/2)(((x−1)/(x+1))))/(sin((π/2)(((x−1)/(x+1)))))))=(8/π)×1= determinant (((8/π)))
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{cos}\left(\frac{\pi}{{x}+\mathrm{1}}\right)}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)}{\mathrm{cos}\left(\frac{\pi}{{x}+\mathrm{1}}\right)}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{{x}+\mathrm{1}}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)}{\mathrm{sin}\left(\frac{\pi\left({x}−\mathrm{1}\right)}{\mathrm{2}\left({x}+\mathrm{1}\right)}\right)}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{2}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\pi}\centerdot\frac{\frac{\pi}{\mathrm{2}}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{2}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\pi}\centerdot\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\frac{\pi}{\mathrm{2}}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)\right)}\right)=\frac{\mathrm{8}}{\pi}×\mathrm{1}=\begin{array}{|c|}{\frac{\mathrm{8}}{\pi}}\\\hline\end{array} \\ $$
Answered by Ar Brandon last updated on 20/Dec/21
lim_(x→2) ((x^3 −8+sinπx)/(2−x))=lim_(x→2) (((x−2)(x^2 +2x+4))/(2−x))+lim_(u→0) ((sin(π(2−u)))/u) =−12+lim_(u→0) ((sin(−πu))/u)=−12−lim_(u→0) π∙((sin(πu))/(πu))=−(π+12)
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{{x}^{\mathrm{3}} −\mathrm{8}+\mathrm{sin}\pi{x}}{\mathrm{2}−{x}}=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)}{\mathrm{2}−{x}}+\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\left(\pi\left(\mathrm{2}−{u}\right)\right)}{{u}} \\ $$$$=−\mathrm{12}+\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\left(−\pi{u}\right)}{{u}}=−\mathrm{12}−\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\pi\centerdot\frac{\mathrm{sin}\left(\pi{u}\right)}{\pi{u}}=−\left(\pi+\mathrm{12}\right) \\ $$
Answered by mathmax by abdo last updated on 20/Dec/21
f(x)=((1−sin((π/x)))/(x^2 −4x+4)) changement (π/x)=t give x=(π/t) f(x)=((1−sint)/((π^2 /t^2 )−((4π)/t)+4))=((t^2 (1−sint))/(π^2 −4πt +4t^2 )) (t→(π/2)) =_(t−(π/2)=z) (((z+(π/2))^2 (1−cosz))/(4(z+(π/2))^2 −4π(z+(π/2))+π^2 ))=Ψ(z) (z→0) Ψ(z)∼(z^2 /2)×(((z+(π/2))^2 )/(4(z^2 +πz+(π^2 /4))−4πz−π^2 )) ⇒ Ψ(z)∼((z^2 (z+(π/2))^2 )/(2{4z^2 +4πz+π^2 −4πz−π^2 }))∼(1/8)(z+(π/2))^2 ⇒lim_(z→0) Ψ(z)=(1/8)(π^2 /4)=(π^2 /(32))=limf(x)
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}−\mathrm{sin}\left(\frac{\pi}{\mathrm{x}}\right)}{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{4}}\:\:\mathrm{changement}\:\frac{\pi}{\mathrm{x}}=\mathrm{t}\:\mathrm{give}\:\mathrm{x}=\frac{\pi}{\mathrm{t}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}−\mathrm{sint}}{\frac{\pi^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} }−\frac{\mathrm{4}\pi}{\mathrm{t}}+\mathrm{4}}=\frac{\mathrm{t}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sint}\right)}{\pi^{\mathrm{2}} −\mathrm{4}\pi\mathrm{t}\:+\mathrm{4t}^{\mathrm{2}} }\:\:\:\left(\mathrm{t}\rightarrow\frac{\pi}{\mathrm{2}}\right) \\ $$$$=_{\mathrm{t}−\frac{\pi}{\mathrm{2}}=\mathrm{z}} \:\:\:\:\:\frac{\left(\mathrm{z}+\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cosz}\right)}{\mathrm{4}\left(\mathrm{z}+\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{4}\pi\left(\mathrm{z}+\frac{\pi}{\mathrm{2}}\right)+\pi^{\mathrm{2}} }=\Psi\left(\mathrm{z}\right)\:\left(\mathrm{z}\rightarrow\mathrm{0}\right) \\ $$$$\Psi\left(\mathrm{z}\right)\sim\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{2}}×\frac{\left(\mathrm{z}+\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{4}\left(\mathrm{z}^{\mathrm{2}} +\pi\mathrm{z}+\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\right)−\mathrm{4}\pi\mathrm{z}−\pi^{\mathrm{2}} }\:\Rightarrow \\ $$$$\Psi\left(\mathrm{z}\right)\sim\frac{\mathrm{z}^{\mathrm{2}} \left(\mathrm{z}+\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}\left\{\mathrm{4z}^{\mathrm{2}} +\mathrm{4}\pi\mathrm{z}+\pi^{\mathrm{2}} −\mathrm{4}\pi\mathrm{z}−\pi^{\mathrm{2}} \right\}}\sim\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{z}+\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{0}} \Psi\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\mathrm{8}}\frac{\pi^{\mathrm{2}} }{\mathrm{4}}=\frac{\pi^{\mathrm{2}} }{\mathrm{32}}=\mathrm{limf}\left(\mathrm{x}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *