Question Number 26289 by d.monhbayr@gmail.com last updated on 23/Dec/17
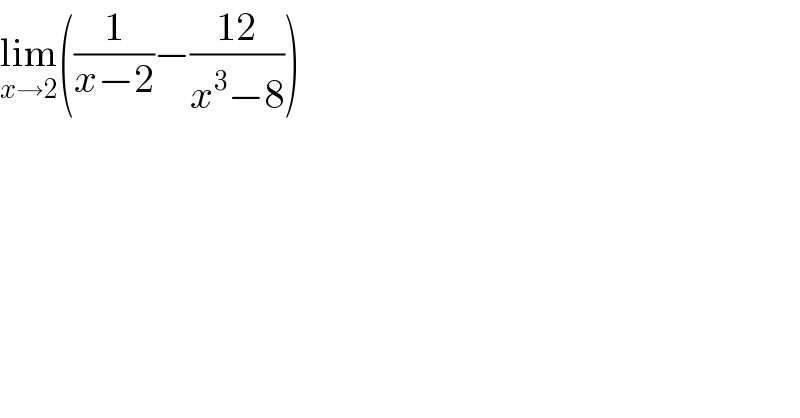
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}−\mathrm{2}}−\frac{\mathrm{12}}{{x}^{\mathrm{3}} −\mathrm{8}}\right) \\ $$
Answered by prakash jain last updated on 24/Dec/17
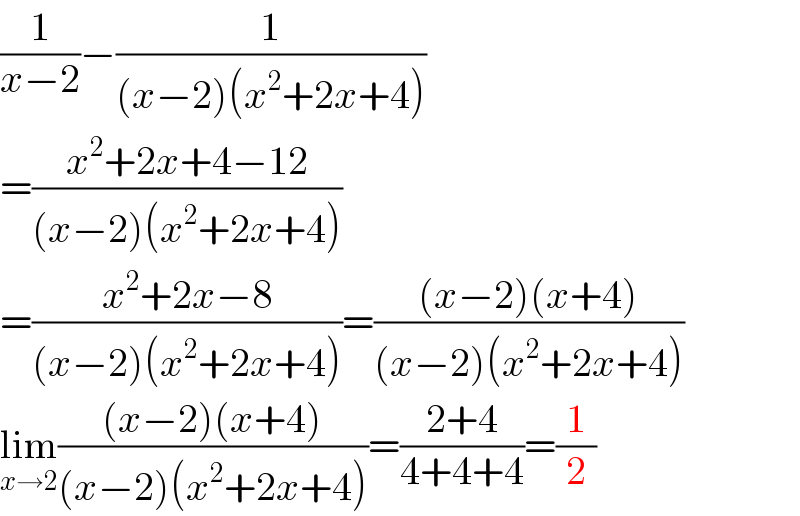
$$\frac{\mathrm{1}}{{x}−\mathrm{2}}−\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)} \\ $$$$=\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}−\mathrm{12}}{\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)} \\ $$$$=\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{8}}{\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)}=\frac{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{4}\right)}{\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{4}\right)}{\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)}=\frac{\mathrm{2}+\mathrm{4}}{\mathrm{4}+\mathrm{4}+\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Rasheed.Sindhi last updated on 24/Dec/17
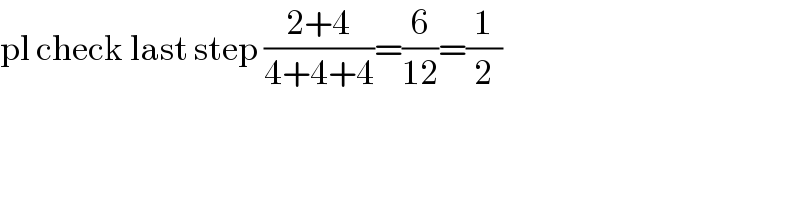
$$\mathrm{pl}\:\mathrm{check}\:\mathrm{last}\:\mathrm{step}\:\frac{\mathrm{2}+\mathrm{4}}{\mathrm{4}+\mathrm{4}+\mathrm{4}}=\frac{\mathrm{6}}{\mathrm{12}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by prakash jain last updated on 24/Dec/17
Thanks Corrected
