Question Number 150202 by tabata last updated on 10/Aug/21
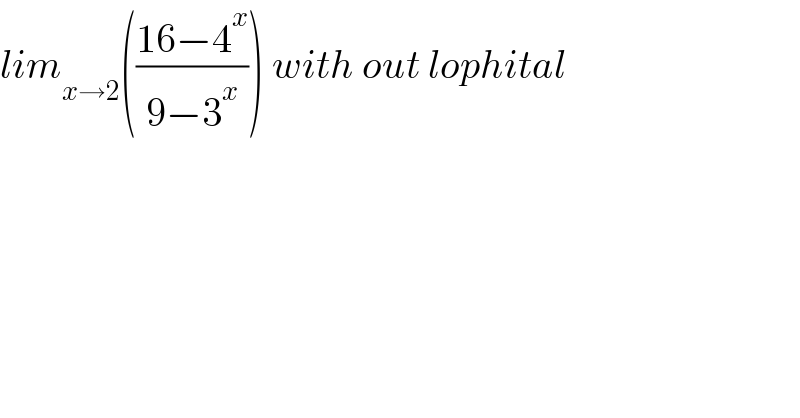
$${lim}_{{x}\rightarrow\mathrm{2}} \left(\frac{\mathrm{16}−\mathrm{4}^{{x}} }{\mathrm{9}−\mathrm{3}^{{x}} }\right)\:{with}\:{out}\:{lophital} \\ $$
Commented by tabata last updated on 10/Aug/21

$$?????? \\ $$
Answered by liberty last updated on 10/Aug/21
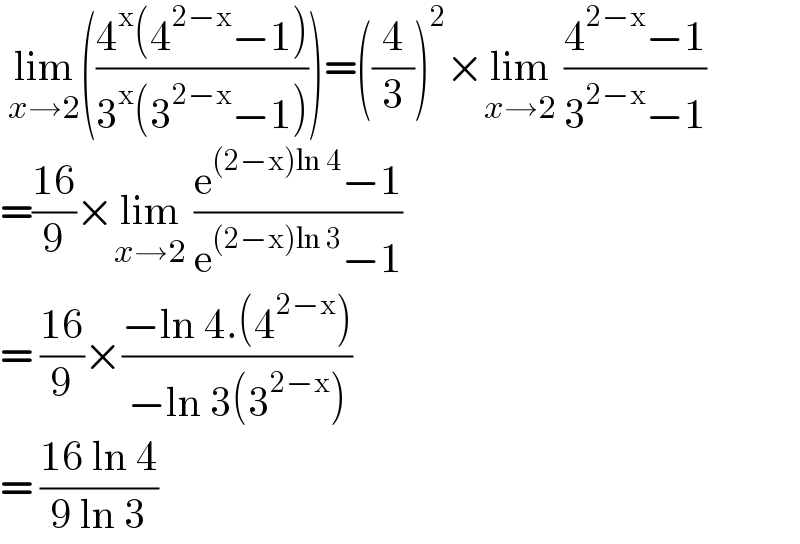
$$\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\left(\frac{\mathrm{4}^{\mathrm{x}} \left(\mathrm{4}^{\mathrm{2}−\mathrm{x}} −\mathrm{1}\right)}{\mathrm{3}^{\mathrm{x}} \left(\mathrm{3}^{\mathrm{2}−\mathrm{x}} −\mathrm{1}\right)}\right)=\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} ×\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{4}^{\mathrm{2}−\mathrm{x}} −\mathrm{1}}{\mathrm{3}^{\mathrm{2}−\mathrm{x}} −\mathrm{1}} \\ $$$$=\frac{\mathrm{16}}{\mathrm{9}}×\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{e}^{\left(\mathrm{2}−\mathrm{x}\right)\mathrm{ln}\:\mathrm{4}} −\mathrm{1}}{\mathrm{e}^{\left(\mathrm{2}−\mathrm{x}\right)\mathrm{ln}\:\mathrm{3}} −\mathrm{1}} \\ $$$$=\:\frac{\mathrm{16}}{\mathrm{9}}×\frac{−\mathrm{ln}\:\mathrm{4}.\left(\mathrm{4}^{\mathrm{2}−\mathrm{x}} \right)}{−\mathrm{ln}\:\mathrm{3}\left(\mathrm{3}^{\mathrm{2}−\mathrm{x}} \right)} \\ $$$$=\:\frac{\mathrm{16}\:\mathrm{ln}\:\mathrm{4}}{\mathrm{9}\:\mathrm{ln}\:\mathrm{3}} \\ $$
Commented by tabata last updated on 10/Aug/21

$${where}\:{the}\:{complete}\:{solution}\: \\ $$
Commented by tabata last updated on 10/Aug/21

$${thank}\:{you}\:{alot} \\ $$
Commented by tabata last updated on 10/Aug/21
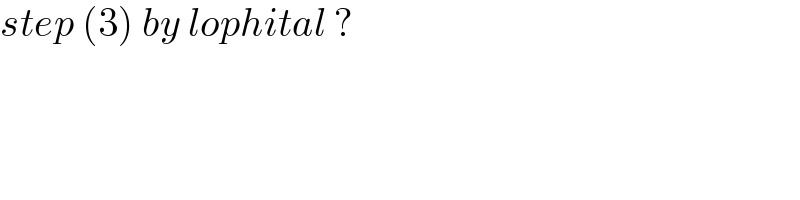
$${step}\:\left(\mathrm{3}\right)\:{by}\:{lophital}\:? \\ $$
Answered by puissant last updated on 10/Aug/21

$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{2}} \left(\frac{\mathrm{16}−\mathrm{e}^{\mathrm{xln4}} }{\mathrm{9}−\mathrm{e}^{\mathrm{xln3}} }\right)\:=\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{2}} \frac{−\mathrm{ln4e}^{\mathrm{xln4}} }{−\mathrm{ln3e}^{\mathrm{xln3}} }\:\left(\mathrm{hopital}\right) \\ $$$$\Rightarrow\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{2}} \left(\frac{\mathrm{16}−\mathrm{4}^{\mathrm{x}} }{\mathrm{9}−\mathrm{3}^{\mathrm{x}} }\right)=\:\frac{\mathrm{ln4}}{\mathrm{ln3}}×\frac{\mathrm{e}^{\mathrm{2ln4}} }{\mathrm{e}^{\mathrm{2ln3}} } \\ $$$$=\:\frac{\mathrm{16}}{\mathrm{9}}\mathrm{log}_{\mathrm{3}} \left(\mathrm{4}\right).. \\ $$
