Question Number 161538 by mnjuly1970 last updated on 19/Dec/21

$$ \\ $$$${lim}_{\:{x}\:\rightarrow\:−\mathrm{2}\:\:} \left(\frac{\mathrm{2}+\:\mathrm{3}{x}\:+\:\mathrm{3}{x}^{\:\mathrm{2}} \:+\:{x}^{\:\mathrm{3}} }{\:{sin}\:\left(\:\frac{\pi{x}}{\mathrm{2}}\:\right)}\:\right)=? \\ $$$$\:\:\:\:−−−− \\ $$
Answered by Ar Brandon last updated on 19/Dec/21
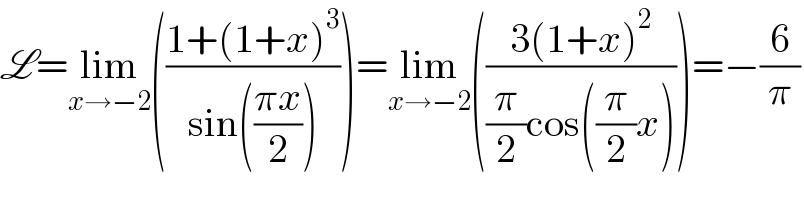
$$\mathscr{L}=\underset{{x}\rightarrow−\mathrm{2}} {\mathrm{lim}}\left(\frac{\mathrm{1}+\left(\mathrm{1}+{x}\right)^{\mathrm{3}} }{\mathrm{sin}\left(\frac{\pi{x}}{\mathrm{2}}\right)}\right)=\underset{{x}\rightarrow−\mathrm{2}} {\mathrm{lim}}\left(\frac{\mathrm{3}\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{\frac{\pi}{\mathrm{2}}\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}{x}\right)}\right)=−\frac{\mathrm{6}}{\pi} \\ $$
Commented by mnjuly1970 last updated on 19/Dec/21
$$\:\:{thx}\:{sir}\:{brandon}.. \\ $$
Answered by cortano last updated on 19/Dec/21
![lim_(x→−2) (((x^3 +3x^2 +3x+2)/(sin (((πx)/2))))) = lim_(x→−2) (((1+(x+1)^3 )/(sin (((πx)/2))))) [ let x+2 = c ] = lim_(c→0) ((1+(c−1)^3 )/(sin (π/2)(c−2))) = lim_(c→0) ((1−(1−c)^3 )/(−sin (π−((πc)/2)))) = lim_(c→0) ((1−(1−3c))/(−sin ((πc)/2))) = −(6/π)](https://www.tinkutara.com/question/Q161548.png)
$$\:\:\underset{{x}\rightarrow−\mathrm{2}} {\mathrm{lim}}\:\left(\frac{{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{2}}{\mathrm{sin}\:\left(\frac{\pi{x}}{\mathrm{2}}\right)}\right)\: \\ $$$$\:\:=\:\underset{{x}\rightarrow−\mathrm{2}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}+\left({x}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{sin}\:\left(\frac{\pi{x}}{\mathrm{2}}\right)}\right) \\ $$$$\:\left[\:{let}\:{x}+\mathrm{2}\:=\:{c}\:\right] \\ $$$$\:\:=\:\underset{{c}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}+\left({c}−\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{sin}\:\frac{\pi}{\mathrm{2}}\left({c}−\mathrm{2}\right)} \\ $$$$\:\:=\:\underset{{c}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−{c}\right)^{\mathrm{3}} }{−\mathrm{sin}\:\left(\pi−\frac{\pi{c}}{\mathrm{2}}\right)} \\ $$$$\:\:=\:\underset{{c}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−\mathrm{3}{c}\right)}{−\mathrm{sin}\:\frac{\pi{c}}{\mathrm{2}}}\:=\:−\frac{\mathrm{6}}{\pi} \\ $$
Commented by mnjuly1970 last updated on 19/Dec/21
$$\:\:\:{thank}\:{you}\:\:{sir}.. \\ $$
