Question Number 102034 by Study last updated on 06/Jul/20
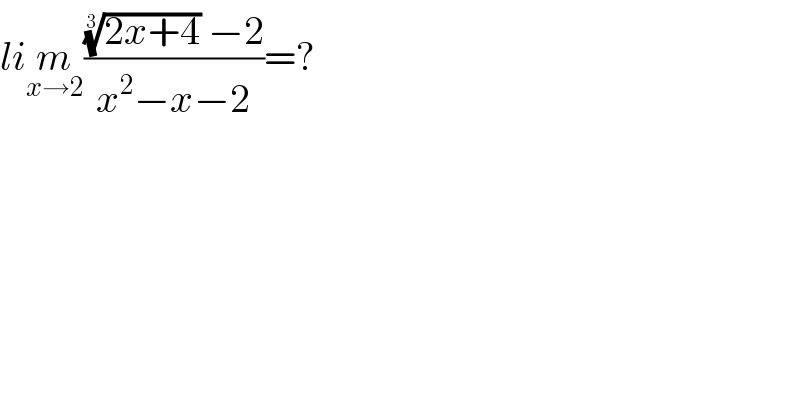
$${li}\underset{{x}\rightarrow\mathrm{2}} {{m}}\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}{x}+\mathrm{4}}\:−\mathrm{2}}{{x}^{\mathrm{2}} −{x}−\mathrm{2}}=? \\ $$
Answered by Dwaipayan Shikari last updated on 06/Jul/20
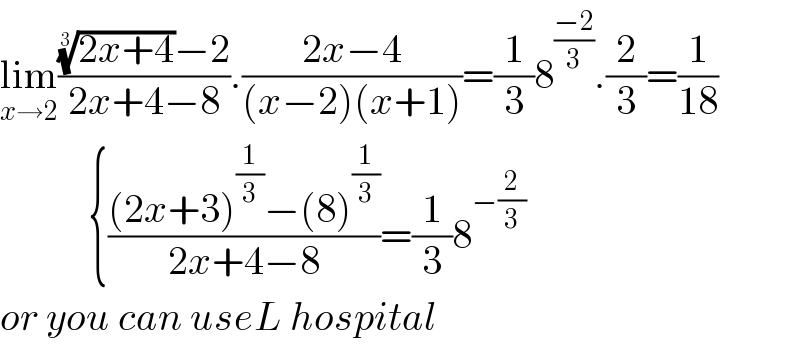
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}{x}+\mathrm{4}}−\mathrm{2}}{\mathrm{2}{x}+\mathrm{4}−\mathrm{8}}.\frac{\mathrm{2}{x}−\mathrm{4}}{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{8}^{\frac{−\mathrm{2}}{\mathrm{3}}} .\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{18}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left\{\frac{\left(\mathrm{2}{x}+\mathrm{3}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\left(\mathrm{8}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{\mathrm{2}{x}+\mathrm{4}−\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{8}^{−\frac{\mathrm{2}}{\mathrm{3}}} \right. \\ $$$${or}\:{you}\:{can}\:{useL}\:{hospital} \\ $$
Commented by Study last updated on 06/Jul/20
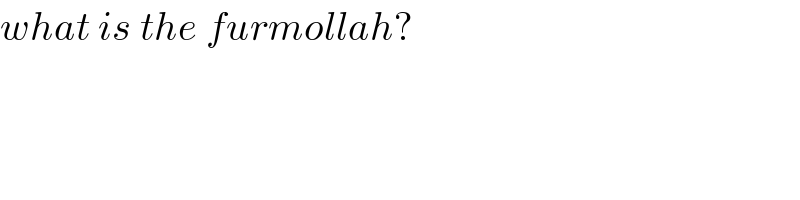
$${what}\:{is}\:{the}\:{furmollah}? \\ $$
Answered by bemath last updated on 06/Jul/20
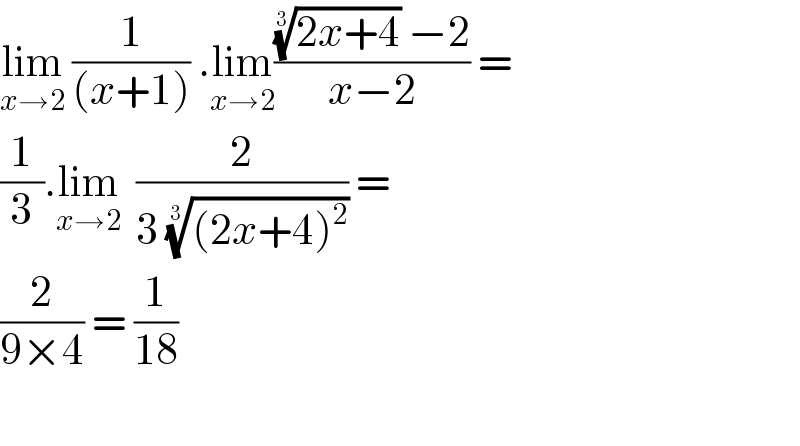
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)}\:.\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}{x}+\mathrm{4}}\:−\mathrm{2}}{{x}−\mathrm{2}}\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}.\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\:\frac{\mathrm{2}}{\mathrm{3}\:\sqrt[{\mathrm{3}}]{\left(\mathrm{2}{x}+\mathrm{4}\right)^{\mathrm{2}} }}\:=\: \\ $$$$\frac{\mathrm{2}}{\mathrm{9}×\mathrm{4}}\:=\:\frac{\mathrm{1}}{\mathrm{18}} \\ $$$$ \\ $$
