Question Number 149871 by ArielVyny last updated on 07/Aug/21

$${lim}_{{x}\rightarrow\mathrm{2}} \frac{\mathrm{3}^{{x}!} −\mathrm{9}}{{x}−\mathrm{2}} \\ $$
Answered by Ar Brandon last updated on 08/Aug/21
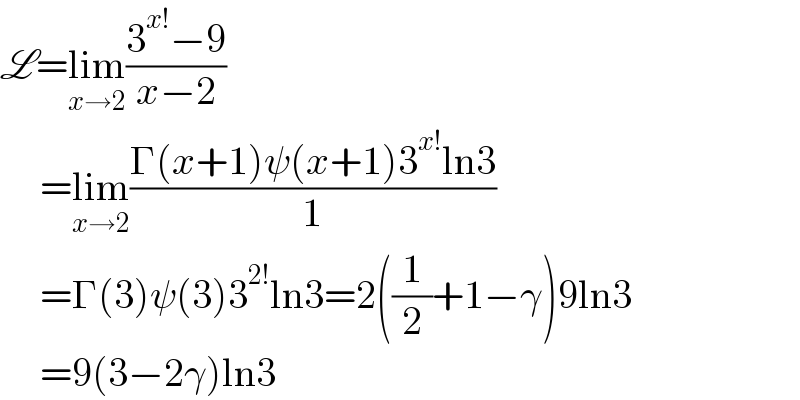
$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{3}^{{x}!} −\mathrm{9}}{{x}−\mathrm{2}} \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\Gamma\left({x}+\mathrm{1}\right)\psi\left({x}+\mathrm{1}\right)\mathrm{3}^{{x}!} \mathrm{ln3}}{\mathrm{1}} \\ $$$$\:\:\:\:\:=\Gamma\left(\mathrm{3}\right)\psi\left(\mathrm{3}\right)\mathrm{3}^{\mathrm{2}!} \mathrm{ln3}=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}−\gamma\right)\mathrm{9ln3} \\ $$$$\:\:\:\:\:=\mathrm{9}\left(\mathrm{3}−\mathrm{2}\gamma\right)\mathrm{ln3} \\ $$
Commented by ArielVyny last updated on 08/Aug/21

$${thank}\:{sir} \\ $$
