Question Number 78791 by jagoll last updated on 20/Jan/20
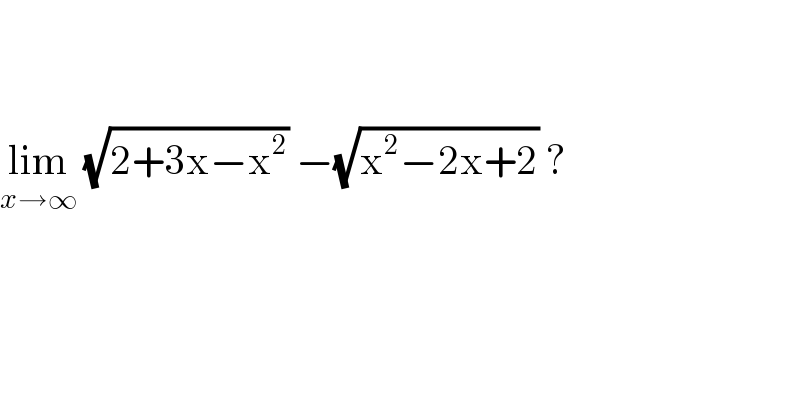
$$ \\ $$$$ \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{2}+\mathrm{3x}−\mathrm{x}^{\mathrm{2}} }\:−\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}}\:? \\ $$
Answered by john santu last updated on 20/Jan/20
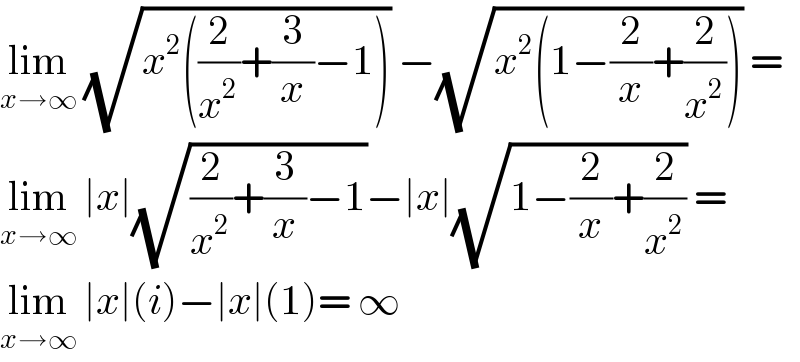
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{{x}^{\mathrm{2}} \left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} }+\frac{\mathrm{3}}{{x}}−\mathrm{1}\right)}\:−\sqrt{{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{2}}{{x}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\right)}\:= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mid{x}\mid\sqrt{\frac{\mathrm{2}}{{x}^{\mathrm{2}} }+\frac{\mathrm{3}}{{x}}−\mathrm{1}}−\mid{x}\mid\sqrt{\mathrm{1}−\frac{\mathrm{2}}{{x}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} }}\:= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mid{x}\mid\left({i}\right)−\mid{x}\mid\left(\mathrm{1}\right)=\:\infty \\ $$
