Question Number 107828 by Rohit@Thakur last updated on 12/Aug/20
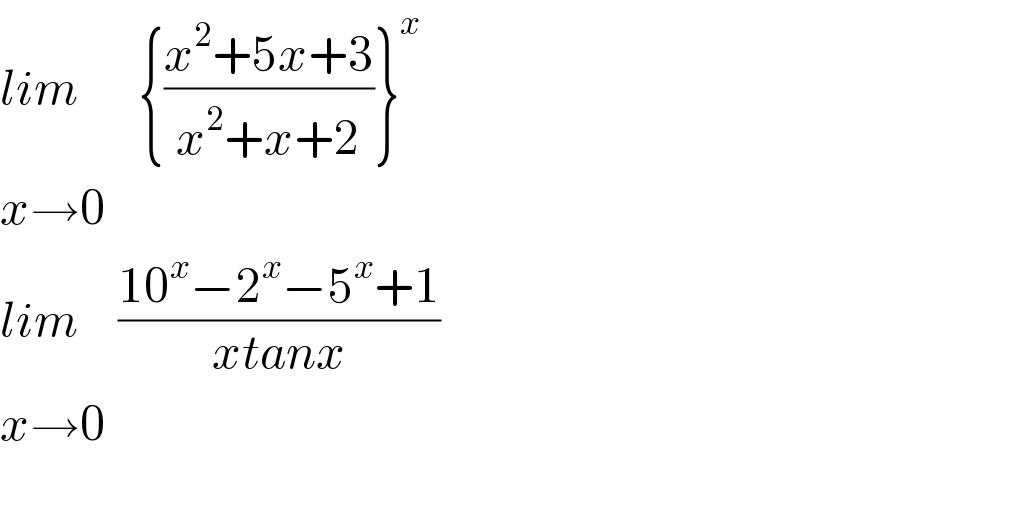
$${lim}\:\:\:\:\:\:\left\{\frac{{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{3}}{{x}^{\mathrm{2}} +{x}+\mathrm{2}}\right\}^{{x}} \\ $$$${x}\rightarrow\mathrm{0} \\ $$$${lim}\:\:\:\:\frac{\mathrm{10}^{{x}} −\mathrm{2}^{{x}} −\mathrm{5}^{{x}} +\mathrm{1}}{{xtanx}} \\ $$$${x}\rightarrow\mathrm{0} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 12/Aug/20
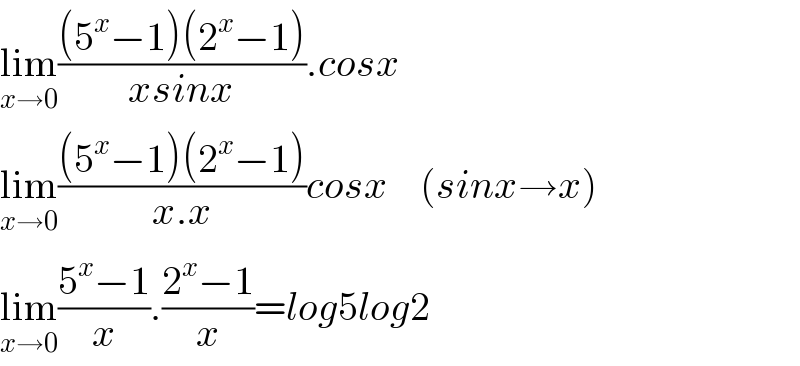
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{5}^{{x}} −\mathrm{1}\right)\left(\mathrm{2}^{{x}} −\mathrm{1}\right)}{{xsinx}}.{cosx}\:\:\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{5}^{{x}} −\mathrm{1}\right)\left(\mathrm{2}^{{x}} −\mathrm{1}\right)}{{x}.{x}}{cosx}\:\:\:\:\left({sinx}\rightarrow{x}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{5}^{{x}} −\mathrm{1}}{{x}}.\frac{\mathrm{2}^{{x}} −\mathrm{1}}{{x}}={log}\mathrm{5}{log}\mathrm{2} \\ $$
Answered by mathmax by abdo last updated on 13/Aug/20
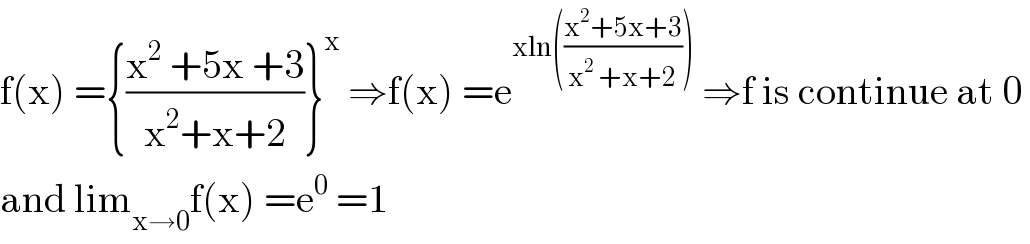
$$\mathrm{f}\left(\mathrm{x}\right)\:=\left\{\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{5x}\:+\mathrm{3}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{2}}\right\}^{\mathrm{x}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\mathrm{xln}\left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{5x}+\mathrm{3}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{2}}\right)} \:\Rightarrow\mathrm{f}\:\mathrm{is}\:\mathrm{continue}\:\mathrm{at}\:\mathrm{0}\: \\ $$$$\mathrm{and}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\mathrm{0}} \:=\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 13/Aug/20
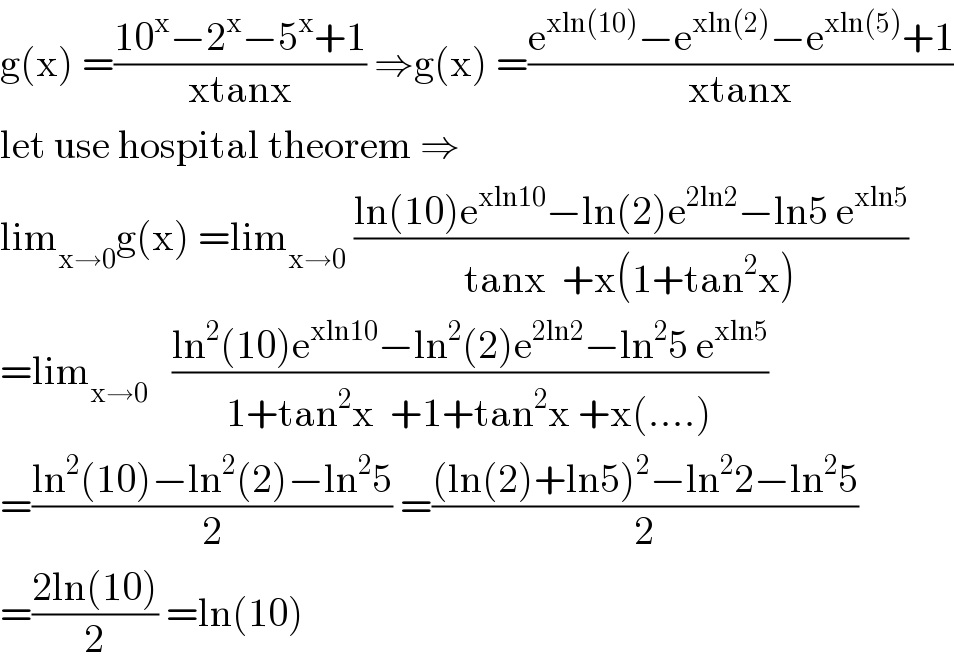
$$\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{10}^{\mathrm{x}} −\mathrm{2}^{\mathrm{x}} −\mathrm{5}^{\mathrm{x}} +\mathrm{1}}{\mathrm{xtanx}}\:\Rightarrow\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{e}^{\mathrm{xln}\left(\mathrm{10}\right)} −\mathrm{e}^{\mathrm{xln}\left(\mathrm{2}\right)} −\mathrm{e}^{\mathrm{xln}\left(\mathrm{5}\right)} +\mathrm{1}}{\mathrm{xtanx}} \\ $$$$\mathrm{let}\:\mathrm{use}\:\mathrm{hospital}\:\mathrm{theorem}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{g}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\frac{\mathrm{ln}\left(\mathrm{10}\right)\mathrm{e}^{\mathrm{xln10}} −\mathrm{ln}\left(\mathrm{2}\right)\mathrm{e}^{\mathrm{2ln2}} −\mathrm{ln5}\:\mathrm{e}^{\mathrm{xln5}} }{\mathrm{tanx}\:\:+\mathrm{x}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{10}\right)\mathrm{e}^{\mathrm{xln10}} −\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)\mathrm{e}^{\mathrm{2ln2}} −\mathrm{ln}^{\mathrm{2}} \mathrm{5}\:\mathrm{e}^{\mathrm{xln5}} }{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\:+\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:+\mathrm{x}\left(….\right)} \\ $$$$=\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{10}\right)−\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{ln}^{\mathrm{2}} \mathrm{5}}{\mathrm{2}}\:=\frac{\left(\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{ln5}\right)^{\mathrm{2}} −\mathrm{ln}^{\mathrm{2}} \mathrm{2}−\mathrm{ln}^{\mathrm{2}} \mathrm{5}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{2ln}\left(\mathrm{10}\right)}{\mathrm{2}}\:=\mathrm{ln}\left(\mathrm{10}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 13/Aug/20
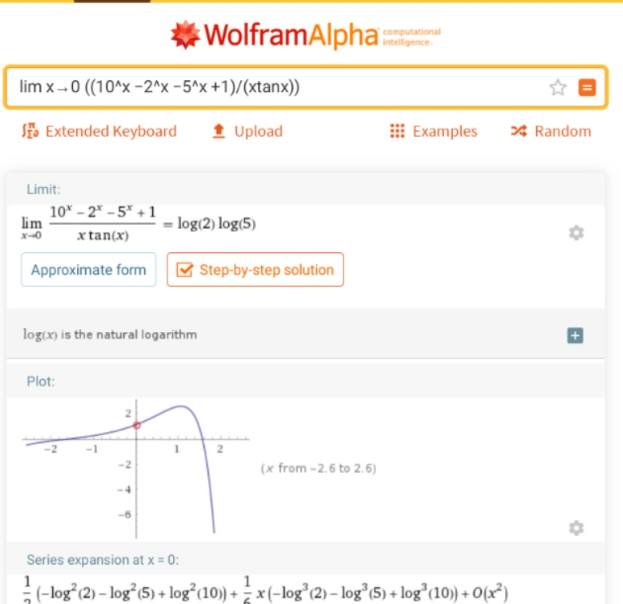
Commented by Dwaipayan Shikari last updated on 13/Aug/20

$${How}\:{sir}? \\ $$
