Question Number 126824 by MathSh last updated on 24/Dec/20
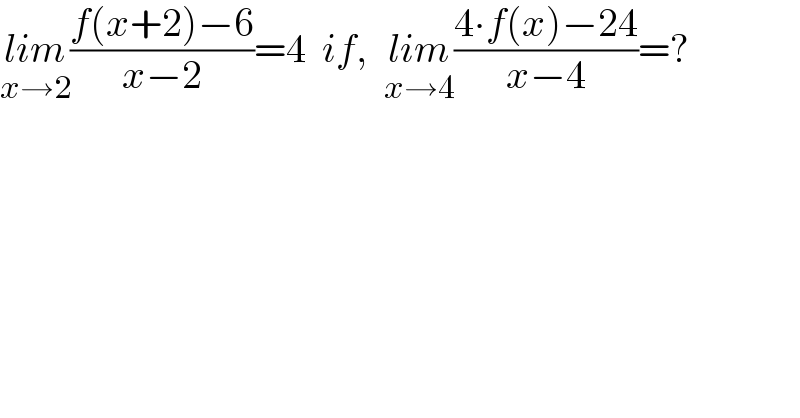
$$\underset{{x}\rightarrow\mathrm{2}} {{lim}}\frac{{f}\left({x}+\mathrm{2}\right)−\mathrm{6}}{{x}−\mathrm{2}}=\mathrm{4}\:\:{if},\:\:\underset{{x}\rightarrow\mathrm{4}} {{lim}}\frac{\mathrm{4}\centerdot{f}\left({x}\right)−\mathrm{24}}{{x}−\mathrm{4}}=? \\ $$
Answered by mahdipoor last updated on 24/Dec/20
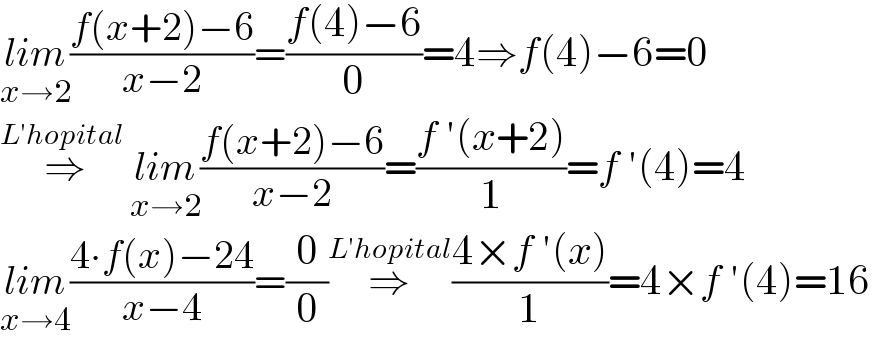
$$\underset{{x}\rightarrow\mathrm{2}} {{lim}}\frac{{f}\left({x}+\mathrm{2}\right)−\mathrm{6}}{{x}−\mathrm{2}}=\frac{{f}\left(\mathrm{4}\right)−\mathrm{6}}{\mathrm{0}}=\mathrm{4}\Rightarrow{f}\left(\mathrm{4}\right)−\mathrm{6}=\mathrm{0} \\ $$$$\overset{{L}'{hopital}\:} {\Rightarrow}\underset{{x}\rightarrow\mathrm{2}} {{lim}}\frac{{f}\left({x}+\mathrm{2}\right)−\mathrm{6}}{{x}−\mathrm{2}}=\frac{{f}\:'\left({x}+\mathrm{2}\right)}{\mathrm{1}}={f}\:'\left(\mathrm{4}\right)=\mathrm{4} \\ $$$$\underset{{x}\rightarrow\mathrm{4}} {{lim}}\frac{\mathrm{4}\centerdot{f}\left({x}\right)−\mathrm{24}}{{x}−\mathrm{4}}=\frac{\mathrm{0}}{\mathrm{0}}\overset{{L}'{hopital}} {\Rightarrow}\frac{\mathrm{4}×{f}\:'\left({x}\right)}{\mathrm{1}}=\mathrm{4}×{f}\:'\left(\mathrm{4}\right)=\mathrm{16} \\ $$
Commented by MathSh last updated on 24/Dec/20

$${Sir},\:{f}'\left(\mathrm{4}\right)=\mathrm{4} \\ $$$$\mathrm{4}\centerdot\mathrm{4}=\mathrm{16} \\ $$
Commented by mahdipoor last updated on 24/Dec/20

$${oh}!{you}\:{are}\:{right} \\ $$$${thank}\:{for}\:{tip} \\ $$
Commented by MathSh last updated on 24/Dec/20
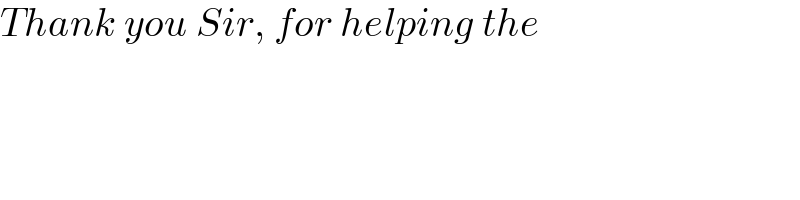
$${Thank}\:{you}\:{Sir},\:{for}\:{helping}\:{the} \\ $$
