Question Number 160256 by qaz last updated on 26/Nov/21
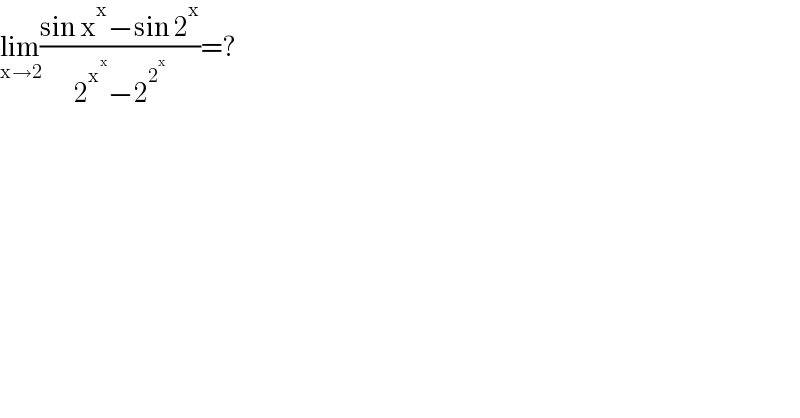
$$\underset{\mathrm{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{x}^{\mathrm{x}} −\mathrm{sin}\:\mathrm{2}^{\mathrm{x}} }{\mathrm{2}^{\mathrm{x}^{\mathrm{x}} } −\mathrm{2}^{\mathrm{2}^{\mathrm{x}} } }=? \\ $$
Commented by cortano last updated on 27/Nov/21
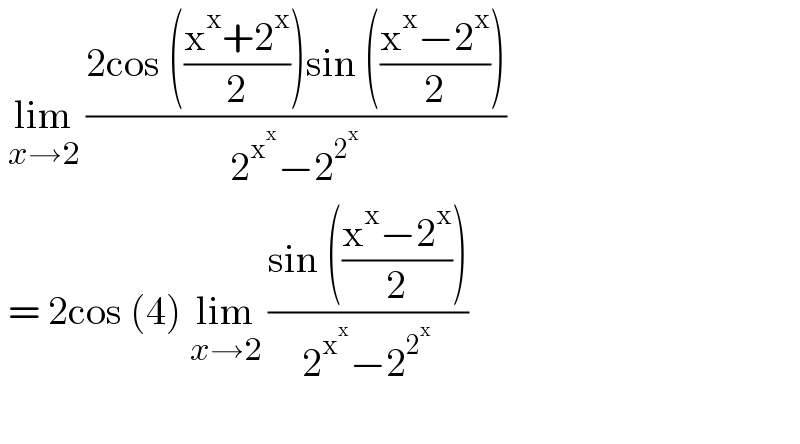
$$\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{2cos}\:\left(\frac{\mathrm{x}^{\mathrm{x}} +\mathrm{2}^{\mathrm{x}} }{\mathrm{2}}\right)\mathrm{sin}\:\left(\frac{\mathrm{x}^{\mathrm{x}} −\mathrm{2}^{\mathrm{x}} }{\mathrm{2}}\right)}{\mathrm{2}^{\mathrm{x}^{\mathrm{x}} } −\mathrm{2}^{\mathrm{2}^{\mathrm{x}} } } \\ $$$$\:=\:\mathrm{2cos}\:\left(\mathrm{4}\right)\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\frac{\mathrm{x}^{\mathrm{x}} −\mathrm{2}^{\mathrm{x}} }{\mathrm{2}}\right)}{\mathrm{2}^{\mathrm{x}^{\mathrm{x}} } −\mathrm{2}^{\mathrm{2}^{\mathrm{x}} } } \\ $$$$\: \\ $$
Commented by qaz last updated on 27/Nov/21
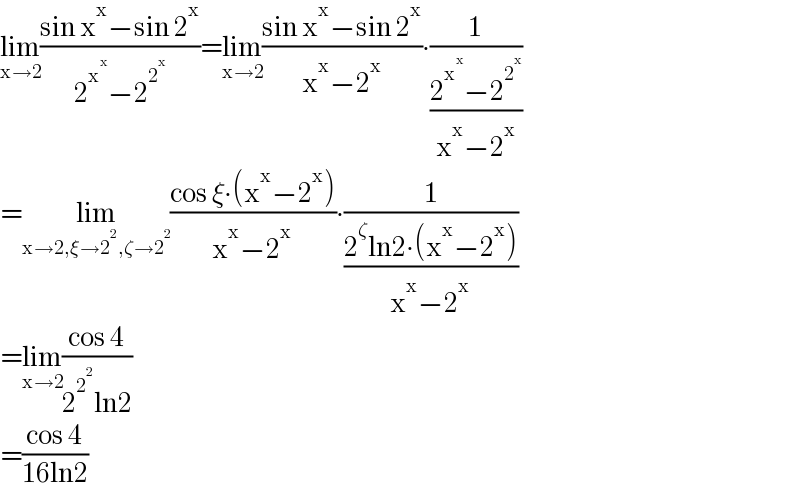
$$\underset{\mathrm{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{x}^{\mathrm{x}} −\mathrm{sin}\:\mathrm{2}^{\mathrm{x}} }{\mathrm{2}^{\mathrm{x}^{\mathrm{x}} } −\mathrm{2}^{\mathrm{2}^{\mathrm{x}} } }=\underset{\mathrm{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{x}^{\mathrm{x}} −\mathrm{sin}\:\mathrm{2}^{\mathrm{x}} }{\mathrm{x}^{\mathrm{x}} −\mathrm{2}^{\mathrm{x}} }\centerdot\frac{\mathrm{1}}{\frac{\mathrm{2}^{\mathrm{x}^{\mathrm{x}} } −\mathrm{2}^{\mathrm{2}^{\mathrm{x}} } }{\mathrm{x}^{\mathrm{x}} −\mathrm{2}^{\mathrm{x}} }} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{2},\xi\rightarrow\mathrm{2}^{\mathrm{2}} ,\zeta\rightarrow\mathrm{2}^{\mathrm{2}} } {\mathrm{lim}}\frac{\mathrm{cos}\:\xi\centerdot\left(\mathrm{x}^{\mathrm{x}} −\mathrm{2}^{\mathrm{x}} \right)}{\mathrm{x}^{\mathrm{x}} −\mathrm{2}^{\mathrm{x}} }\centerdot\frac{\mathrm{1}}{\frac{\mathrm{2}^{\zeta} \mathrm{ln2}\centerdot\left(\mathrm{x}^{\mathrm{x}} −\mathrm{2}^{\mathrm{x}} \right)}{\mathrm{x}^{\mathrm{x}} −\mathrm{2}^{\mathrm{x}} }} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{cos}\:\mathrm{4}}{\mathrm{2}^{\mathrm{2}^{\mathrm{2}} } \mathrm{ln2}} \\ $$$$=\frac{\mathrm{cos}\:\mathrm{4}}{\mathrm{16ln2}} \\ $$
