Question Number 116756 by bemath last updated on 06/Oct/20
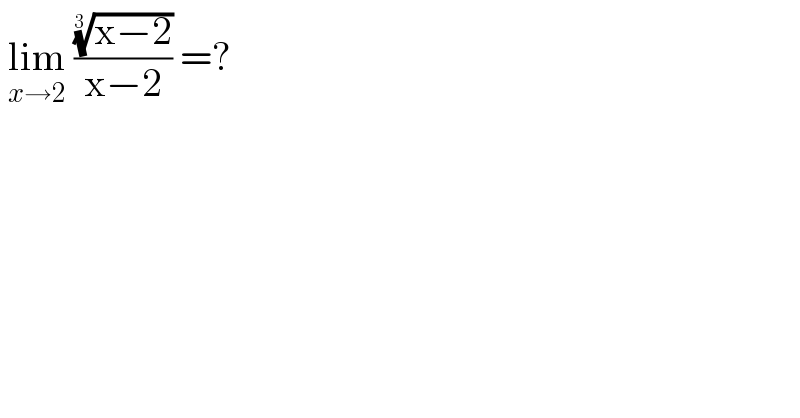
$$\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{x}−\mathrm{2}}}{\mathrm{x}−\mathrm{2}}\:=? \\ $$
Answered by bobhans last updated on 06/Oct/20
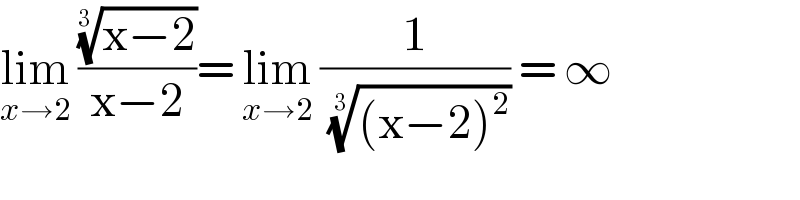
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{x}−\mathrm{2}}}{\mathrm{x}−\mathrm{2}}=\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }}\:=\:\infty \\ $$
Answered by Bird last updated on 07/Oct/20
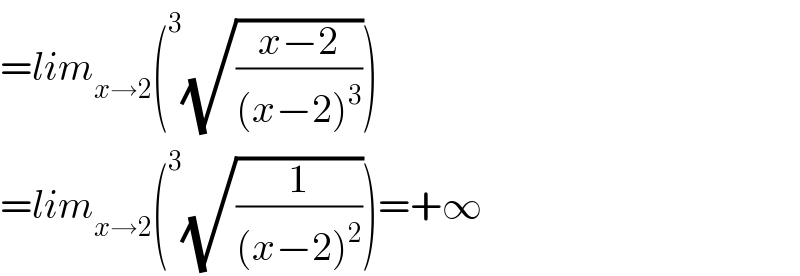
$$={lim}_{{x}\rightarrow\mathrm{2}} \left(^{\mathrm{3}} \sqrt{\frac{{x}−\mathrm{2}}{\left({x}−\mathrm{2}\right)^{\mathrm{3}} }}\right) \\ $$$$={lim}_{{x}\rightarrow\mathrm{2}} \left(^{\mathrm{3}} \sqrt{\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }}\right)=+\infty \\ $$
