Question Number 148694 by liberty last updated on 30/Jul/21
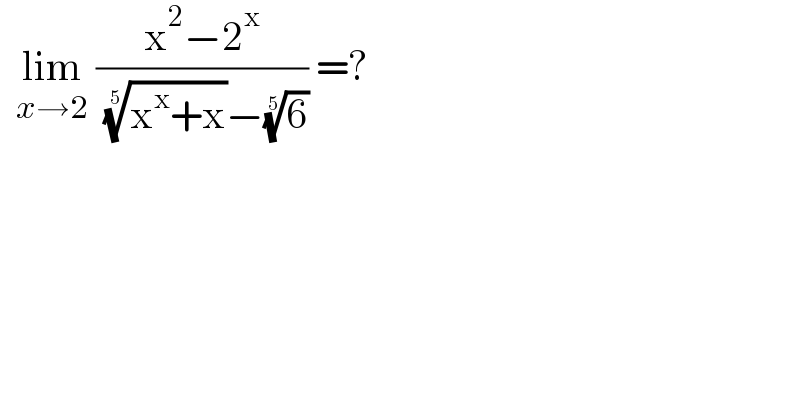
$$\:\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{2}^{\mathrm{x}} }{\:\sqrt[{\mathrm{5}}]{\mathrm{x}^{\mathrm{x}} +\mathrm{x}}−\sqrt[{\mathrm{5}}]{\mathrm{6}}}\:=? \\ $$
Commented by Sozan last updated on 30/Jul/21
![=lim_(x→2) (((2x − 2^x ln(2))/(((x^x [ln(x)+x]+1)/(5(((x^x +x)^4 ))^(1/5) )) ))) =(((4 − 4 ln(2))/(4 [ln(2) +2]+1)) × 5 (6^4 )^(1/5) ) →Sozan](https://www.tinkutara.com/question/Q148709.png)
$$ \\ $$$$={lim}_{{x}\rightarrow\mathrm{2}} \left(\frac{\mathrm{2}{x}\:−\:\mathrm{2}^{{x}} {ln}\left(\mathrm{2}\right)}{\frac{{x}^{{x}} \left[{ln}\left({x}\right)+{x}\right]+\mathrm{1}}{\mathrm{5}\sqrt[{\mathrm{5}}]{\left({x}^{{x}} +{x}\right)^{\mathrm{4}} }}\:}\right) \\ $$$$ \\ $$$$=\left(\frac{\mathrm{4}\:−\:\mathrm{4}\:{ln}\left(\mathrm{2}\right)}{\mathrm{4}\:\left[{ln}\left(\mathrm{2}\right)\:+\mathrm{2}\right]+\mathrm{1}}\:×\:\mathrm{5}\:\sqrt[{\mathrm{5}}]{\mathrm{6}^{\mathrm{4}} }\right) \\ $$$$ \\ $$$$\rightarrow{Sozan} \\ $$
Commented by liberty last updated on 30/Jul/21

$$\mathrm{L}'\mathrm{Hopital} \\ $$
Commented by Sozan last updated on 30/Jul/21

$${yes}\: \\ $$
