Question Number 171247 by ilhamQ last updated on 11/Jun/22
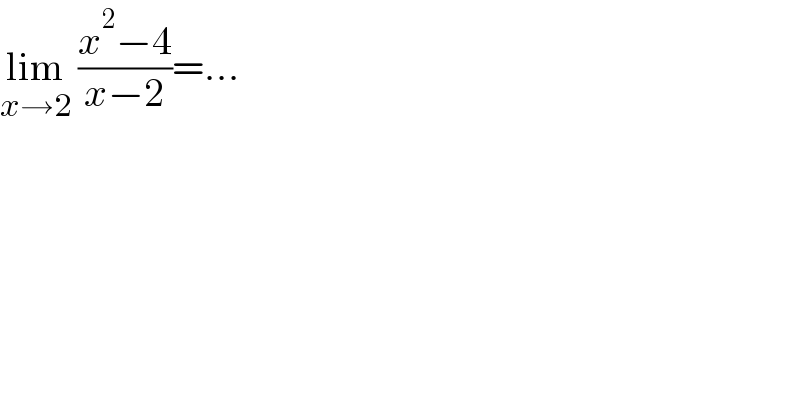
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} −\mathrm{4}}{{x}−\mathrm{2}}=… \\ $$
Answered by Rasheed.Sindhi last updated on 11/Jun/22
![lim_(x→2) ((x^2 −4)/(x−2))=? determinant (((lim_(x→a) ((x^n −a^n )/(x−a))=na^(n−1) ))) lim_(x→2) ((x^2 −4)/(x−2))=lim_(x→2) ((x^2 −2^2 )/(x−2))=2(2)^(2−1) =4 [a=2,n=2]](https://www.tinkutara.com/question/Q171250.png)
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} −\mathrm{4}}{{x}−\mathrm{2}}=? \\ $$$$\begin{array}{|c|}{\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{x}^{{n}} −{a}^{{n}} }{{x}−{a}}={na}^{{n}−\mathrm{1}} }\\\hline\end{array}\: \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} −\mathrm{4}}{{x}−\mathrm{2}}=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }{{x}−\mathrm{2}}=\mathrm{2}\left(\mathrm{2}\right)^{\mathrm{2}−\mathrm{1}} =\mathrm{4} \\ $$$$\left[{a}=\mathrm{2},{n}=\mathrm{2}\right] \\ $$
Commented by peter frank last updated on 11/Jun/22

$$\mathrm{thank}\:\mathrm{you} \\ $$$$ \\ $$
Answered by nurtani last updated on 11/Jun/22
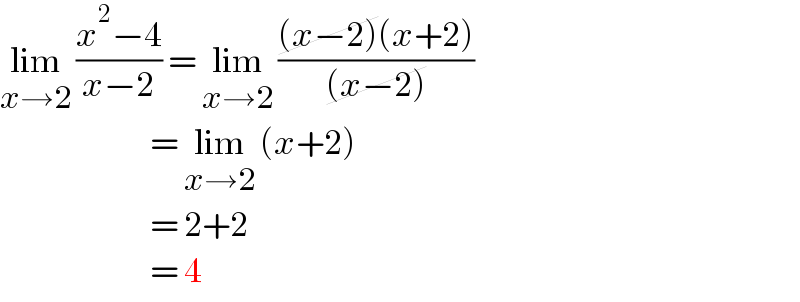
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} −\mathrm{4}}{{x}−\mathrm{2}}\:=\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\cancel{\left({x}−\mathrm{2}\right)}\left({x}+\mathrm{2}\right)}{\cancel{\left({x}−\mathrm{2}\right)}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\left({x}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}+\mathrm{2}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{4} \\ $$
