Question Number 130120 by Study last updated on 22/Jan/21
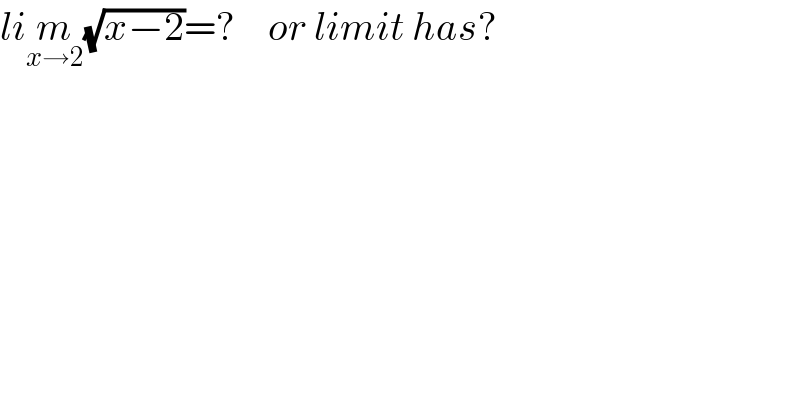
$${li}\underset{{x}\rightarrow\mathrm{2}} {{m}}\sqrt{{x}−\mathrm{2}}=?\:\:\:\:{or}\:{limit}\:{has}? \\ $$
Answered by Olaf last updated on 22/Jan/21
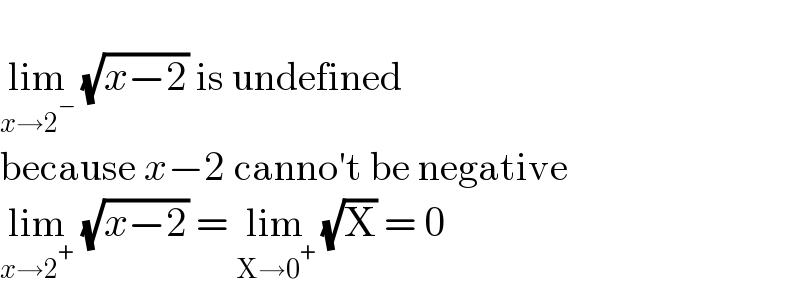
$$ \\ $$$$\underset{{x}\rightarrow\mathrm{2}^{−} } {\mathrm{lim}}\:\sqrt{{x}−\mathrm{2}}\:\mathrm{is}\:\mathrm{undefined} \\ $$$$\mathrm{because}\:{x}−\mathrm{2}\:\mathrm{canno}'\mathrm{t}\:\mathrm{be}\:\mathrm{negative} \\ $$$$\underset{{x}\rightarrow\mathrm{2}^{+} } {\mathrm{lim}}\:\sqrt{{x}−\mathrm{2}}\:=\:\underset{\mathrm{X}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\sqrt{\mathrm{X}}\:=\:\mathrm{0} \\ $$
