Question Number 184883 by mathlove last updated on 13/Jan/23
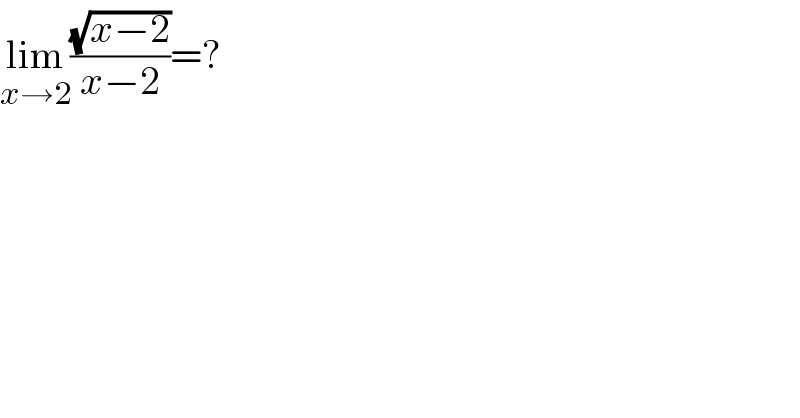
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\sqrt{{x}−\mathrm{2}}}{{x}−\mathrm{2}}=? \\ $$
Answered by aba last updated on 13/Jan/23
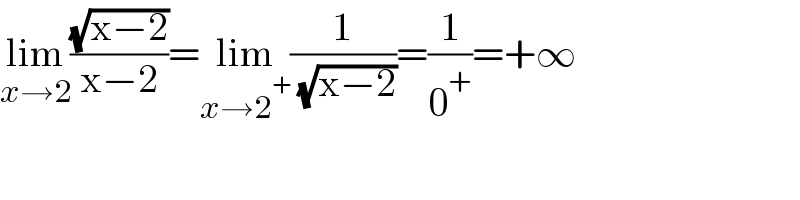
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\sqrt{\mathrm{x}−\mathrm{2}}}{\mathrm{x}−\mathrm{2}}=\underset{{x}\rightarrow\mathrm{2}^{+} } {\mathrm{lim}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}−\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{0}^{+} }=+\infty \\ $$
Commented by Frix last updated on 13/Jan/23
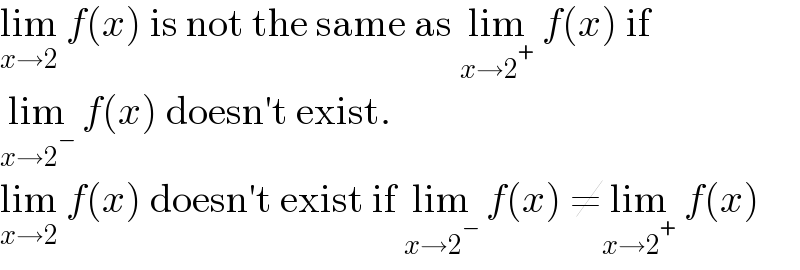
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{not}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\underset{{x}\rightarrow\mathrm{2}^{+} } {\mathrm{lim}}\:{f}\left({x}\right)\:\mathrm{if} \\ $$$$\underset{{x}\rightarrow\mathrm{2}^{−} } {\mathrm{lim}}\:{f}\left({x}\right)\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist}. \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:{f}\left({x}\right)\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist}\:\mathrm{if}\:\underset{{x}\rightarrow\mathrm{2}^{−} } {\mathrm{lim}}\:{f}\left({x}\right)\:\neq\underset{{x}\rightarrow\mathrm{2}^{+} } {\mathrm{lim}}\:{f}\left({x}\right) \\ $$
Commented by aba last updated on 13/Jan/23
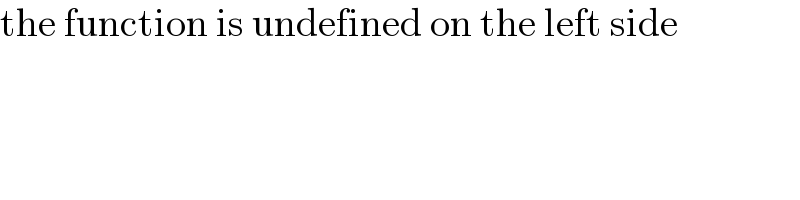
$$\mathrm{the}\:\mathrm{function}\:\mathrm{is}\:\mathrm{undefined}\:\mathrm{on}\:\mathrm{the}\:\mathrm{left}\:\mathrm{side} \\ $$
Commented by Frix last updated on 13/Jan/23
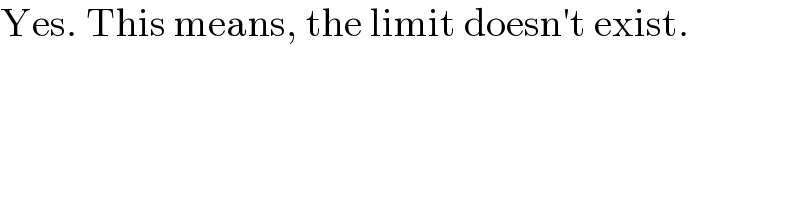
$$\mathrm{Yes}.\:\mathrm{This}\:\mathrm{means},\:\mathrm{the}\:\mathrm{limit}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist}. \\ $$
