Question Number 148439 by liberty last updated on 28/Jul/21
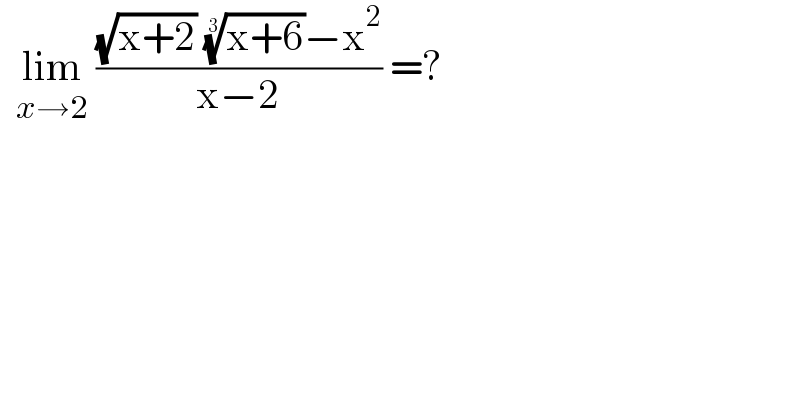
$$\:\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{x}+\mathrm{2}}\:\sqrt[{\mathrm{3}}]{\mathrm{x}+\mathrm{6}}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}−\mathrm{2}}\:=? \\ $$
Answered by dumitrel last updated on 28/Jul/21
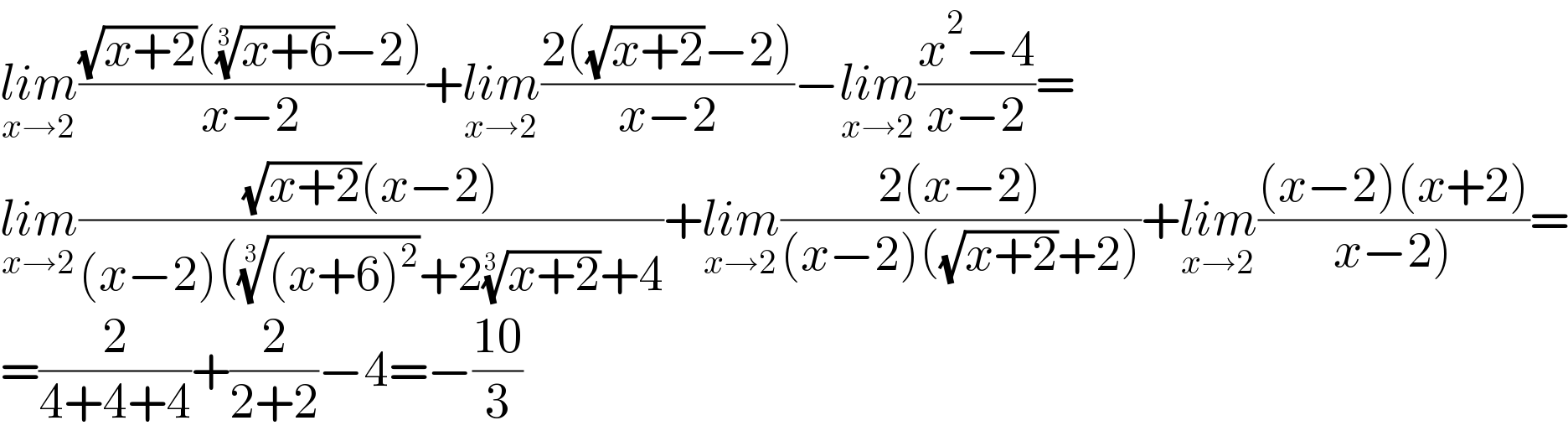
$$\underset{{x}\rightarrow\mathrm{2}} {{lim}}\frac{\sqrt{{x}+\mathrm{2}}\left(\sqrt[{\mathrm{3}}]{{x}+\mathrm{6}}−\mathrm{2}\right)}{{x}−\mathrm{2}}+\underset{{x}\rightarrow\mathrm{2}} {{lim}}\frac{\mathrm{2}\left(\sqrt{{x}+\mathrm{2}}−\mathrm{2}\right)}{{x}−\mathrm{2}}−\underset{{x}\rightarrow\mathrm{2}} {{lim}}\frac{{x}^{\mathrm{2}} −\mathrm{4}}{{x}−\mathrm{2}}= \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {{lim}}\frac{\sqrt{{x}+\mathrm{2}}\left({x}−\mathrm{2}\right)}{\left({x}−\mathrm{2}\right)\left(\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{6}\right)^{\mathrm{2}} }+\mathrm{2}\sqrt[{\mathrm{3}}]{{x}+\mathrm{2}}+\mathrm{4}\right.}+\underset{{x}\rightarrow\mathrm{2}} {{lim}}\frac{\mathrm{2}\left({x}−\mathrm{2}\right)}{\left({x}−\mathrm{2}\right)\left(\sqrt{{x}+\mathrm{2}}+\mathrm{2}\right)}+\underset{{x}\rightarrow\mathrm{2}} {{lim}}\frac{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{2}\right)}{\left.{x}−\mathrm{2}\right)}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{4}+\mathrm{4}+\mathrm{4}}+\frac{\mathrm{2}}{\mathrm{2}+\mathrm{2}}−\mathrm{4}=−\frac{\mathrm{10}}{\mathrm{3}} \\ $$
Answered by EDWIN88 last updated on 28/Jul/21

Answered by mathmax by abdo last updated on 28/Jul/21

$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\sqrt{\mathrm{x}+\mathrm{2}}\left(\mathrm{x}+\mathrm{6}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{x}^{\mathrm{2}} }{\mathrm{x}−\mathrm{2}}\:\mathrm{changement}\:\mathrm{x}−\mathrm{2}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{g}\left(\mathrm{t}\right)=\frac{\sqrt{\mathrm{t}+\mathrm{4}}\left(\mathrm{t}+\mathrm{8}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\left(\mathrm{t}+\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{t}} \\ $$$$=\frac{\sqrt{\mathrm{t}+\mathrm{4}}\left(\mathrm{t}+\mathrm{8}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{t}^{\mathrm{2}} −\mathrm{4t}−\mathrm{4}}{\mathrm{t}}=\frac{\mathrm{2}\sqrt{\mathrm{1}+\frac{\mathrm{t}}{\mathrm{4}}}\left(^{\mathrm{3}} \sqrt{\mathrm{8}}\left(\mathrm{1}+\frac{\mathrm{t}}{\mathrm{8}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{t}^{\mathrm{2}} −\mathrm{4t}−\mathrm{4}\right.}{\mathrm{t}} \\ $$$$\Rightarrow\mathrm{g}\left(\mathrm{t}\right)\sim\frac{\mathrm{4}\left(\mathrm{1}+\frac{\mathrm{t}}{\mathrm{8}}\right)\left(\mathrm{1}+\frac{\mathrm{t}}{\mathrm{24}}\right)−\mathrm{t}^{\mathrm{2}} −\mathrm{4t}−\mathrm{4}}{\mathrm{t}} \\ $$$$=\frac{\mathrm{4}\left(\mathrm{1}+\frac{\mathrm{t}}{\mathrm{24}}+\frac{\mathrm{t}}{\mathrm{8}}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{8}.\mathrm{24}}\right)−\mathrm{t}^{\mathrm{2}} −\mathrm{4t}−\mathrm{4}}{\mathrm{t}} \\ $$$$=\frac{\frac{\mathrm{t}}{\mathrm{6}}+\frac{\mathrm{t}}{\mathrm{2}}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{48}}−\mathrm{t}^{\mathrm{2}} −\mathrm{4t}}{\mathrm{t}}=\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{4}+\left(\frac{\mathrm{t}}{\mathrm{48}}−\mathrm{t}\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}} \mathrm{g}\left(\mathrm{t}\right)=\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{4}\:=−\frac{\mathrm{10}}{\mathrm{3}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\smile\mathrm{2}} \mathrm{f}\left(\mathrm{x}\right)=−\frac{\mathrm{10}}{\mathrm{3}} \\ $$
