Question Number 165699 by lapache last updated on 06/Feb/22
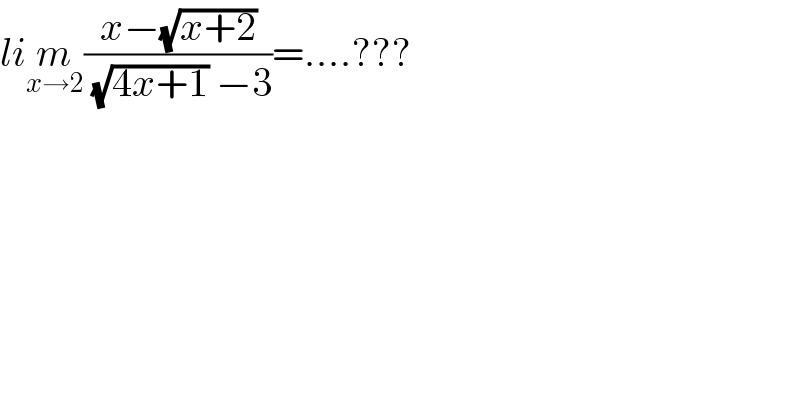
$${li}\underset{{x}\rightarrow\mathrm{2}} {{m}}\frac{{x}−\sqrt{{x}+\mathrm{2}}}{\:\sqrt{\mathrm{4}{x}+\mathrm{1}}\:−\mathrm{3}}=….??? \\ $$
Commented by cortano1 last updated on 07/Feb/22
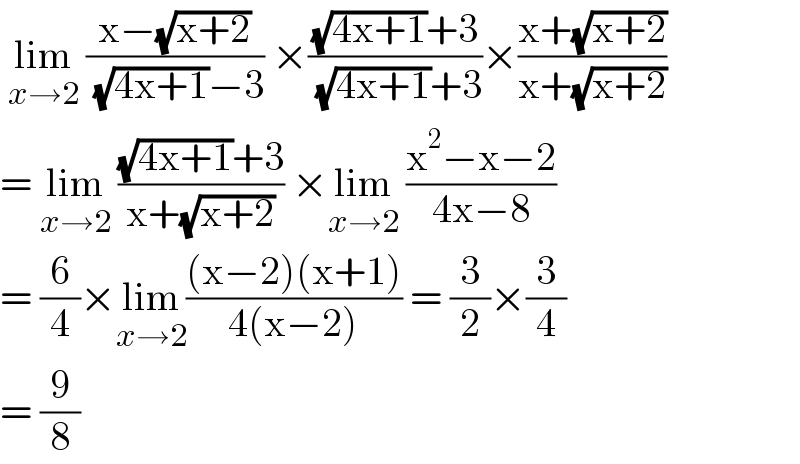
$$\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{x}−\sqrt{\mathrm{x}+\mathrm{2}}}{\:\sqrt{\mathrm{4x}+\mathrm{1}}−\mathrm{3}}\:×\frac{\sqrt{\mathrm{4x}+\mathrm{1}}+\mathrm{3}}{\:\sqrt{\mathrm{4x}+\mathrm{1}}+\mathrm{3}}×\frac{\mathrm{x}+\sqrt{\mathrm{x}+\mathrm{2}}}{\mathrm{x}+\sqrt{\mathrm{x}+\mathrm{2}}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{4x}+\mathrm{1}}+\mathrm{3}}{\mathrm{x}+\sqrt{\mathrm{x}+\mathrm{2}}}\:×\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2}}{\mathrm{4x}−\mathrm{8}} \\ $$$$=\:\frac{\mathrm{6}}{\mathrm{4}}×\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{4}\left(\mathrm{x}−\mathrm{2}\right)}\:=\:\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$=\:\frac{\mathrm{9}}{\mathrm{8}} \\ $$
Answered by nurtani last updated on 06/Feb/22
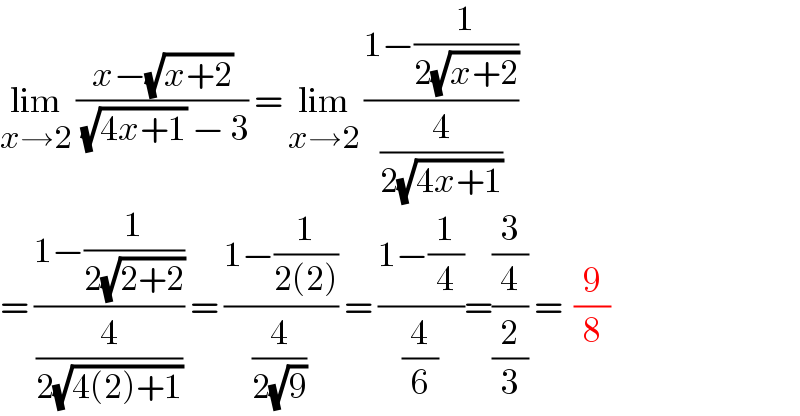
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{x}−\sqrt{{x}+\mathrm{2}}}{\:\sqrt{\mathrm{4}{x}+\mathrm{1}}\:−\:\mathrm{3}}\:=\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\mathrm{2}}}}{\frac{\mathrm{4}}{\mathrm{2}\sqrt{\mathrm{4}{x}+\mathrm{1}}}}\: \\ $$$$=\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}+\mathrm{2}}}}{\frac{\mathrm{4}}{\mathrm{2}\sqrt{\mathrm{4}\left(\mathrm{2}\right)+\mathrm{1}}}}\:=\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}\right)}}{\frac{\mathrm{4}}{\mathrm{2}\sqrt{\mathrm{9}}}}\:=\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}{\frac{\mathrm{4}}{\mathrm{6}}}=\frac{\frac{\mathrm{3}}{\mathrm{4}}}{\frac{\mathrm{2}}{\mathrm{3}}}\:=\:\:\frac{\mathrm{9}}{\mathrm{8}} \\ $$
