Question Number 130854 by mathlove last updated on 29/Jan/21
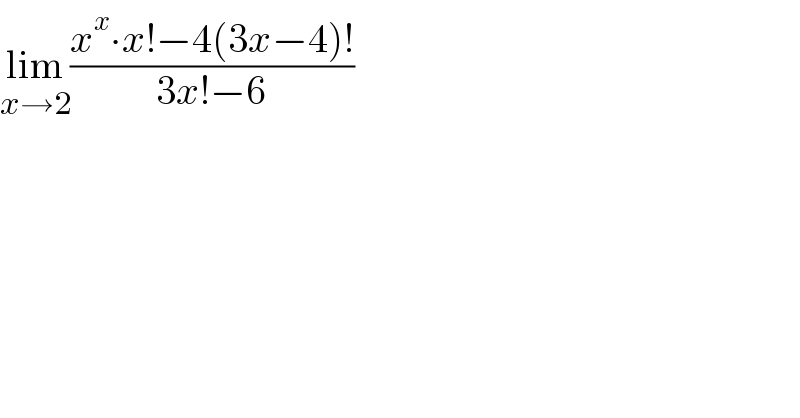
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{{x}^{{x}} \centerdot{x}!−\mathrm{4}\left(\mathrm{3}{x}−\mathrm{4}\right)!}{\mathrm{3}{x}!−\mathrm{6}} \\ $$
Answered by Dwaipayan Shikari last updated on 29/Jan/21
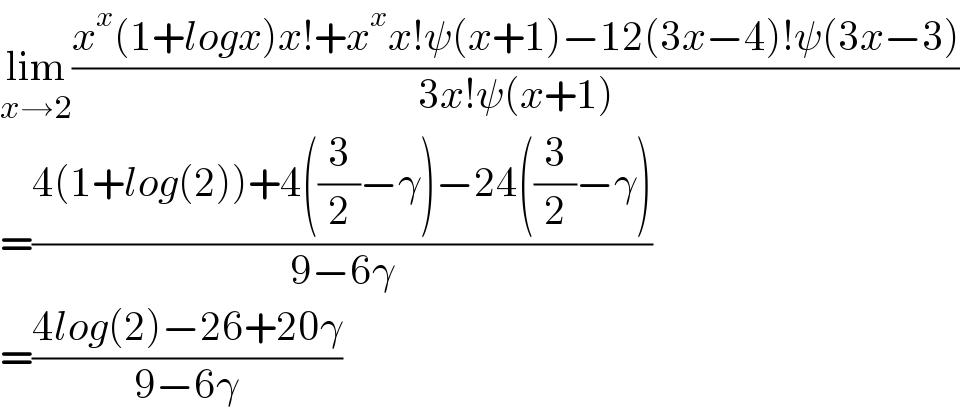
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{{x}^{{x}} \left(\mathrm{1}+{logx}\right){x}!+{x}^{{x}} {x}!\psi\left({x}+\mathrm{1}\right)−\mathrm{12}\left(\mathrm{3}{x}−\mathrm{4}\right)!\psi\left(\mathrm{3}{x}−\mathrm{3}\right)}{\mathrm{3}{x}!\psi\left({x}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{4}\left(\mathrm{1}+{log}\left(\mathrm{2}\right)\right)+\mathrm{4}\left(\frac{\mathrm{3}}{\mathrm{2}}−\gamma\right)−\mathrm{24}\left(\frac{\mathrm{3}}{\mathrm{2}}−\gamma\right)}{\mathrm{9}−\mathrm{6}\gamma} \\ $$$$=\frac{\mathrm{4}{log}\left(\mathrm{2}\right)−\mathrm{26}+\mathrm{20}\gamma}{\mathrm{9}−\mathrm{6}\gamma} \\ $$
Commented by mathlove last updated on 29/Jan/21
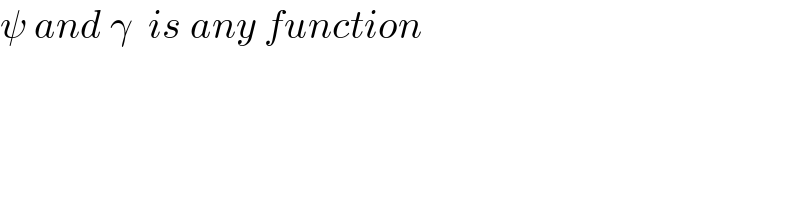
$$\psi\:{and}\:\gamma\:\:{is}\:{any}\:{function} \\ $$
Commented by Dwaipayan Shikari last updated on 29/Jan/21

$$\frac{\Gamma'\left({x}\right)}{\Gamma\left({x}\right)}=\psi\left({x}\right)\:\:\left({Digamma}\:{function}\right) \\ $$$$\psi\left({x}\right)=−\gamma+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+{x}} \\ $$$$\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt}=\left({x}−\mathrm{1}\right)! \\ $$$$\gamma=\mathcal{E}{ulerian}\:{Constant}\:=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}}−{log}\left({n}\right) \\ $$
Commented by mathlove last updated on 29/Jan/21

$${thanks}\:\:{bro} \\ $$
