Question Number 148600 by EDWIN88 last updated on 29/Jul/21
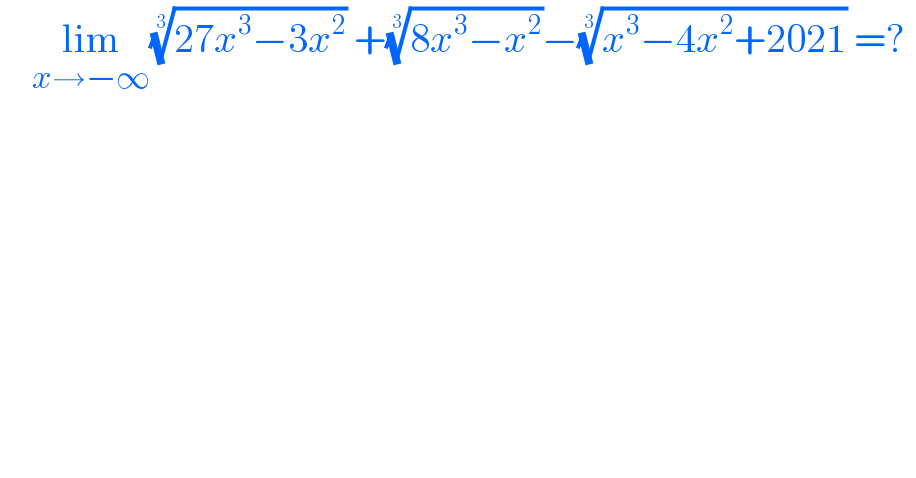
$$\:\:\:\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\sqrt[{\mathrm{3}}]{\mathrm{27}{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} }\:+\sqrt[{\mathrm{3}}]{\mathrm{8}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} }−\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{2021}}\:=?\: \\ $$
Answered by bemath last updated on 29/Jul/21
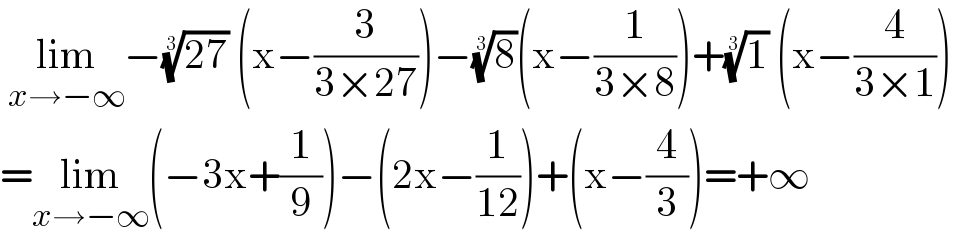
$$\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}−\sqrt[{\mathrm{3}}]{\mathrm{27}}\:\left(\mathrm{x}−\frac{\mathrm{3}}{\mathrm{3}×\mathrm{27}}\right)−\sqrt[{\mathrm{3}}]{\mathrm{8}}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{3}×\mathrm{8}}\right)+\sqrt[{\mathrm{3}}]{\mathrm{1}}\:\left(\mathrm{x}−\frac{\mathrm{4}}{\mathrm{3}×\mathrm{1}}\right) \\ $$$$=\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left(−\mathrm{3x}+\frac{\mathrm{1}}{\mathrm{9}}\right)−\left(\mathrm{2x}−\frac{\mathrm{1}}{\mathrm{12}}\right)+\left(\mathrm{x}−\frac{\mathrm{4}}{\mathrm{3}}\right)=+\infty \\ $$
