Question Number 146263 by bemath last updated on 12/Jul/21
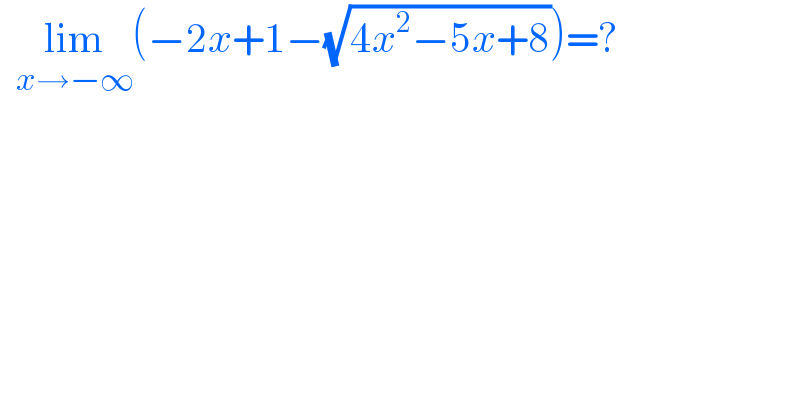
$$\:\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left(−\mathrm{2}{x}+\mathrm{1}−\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{8}}\right)=? \\ $$
Answered by gsk2684 last updated on 12/Jul/21
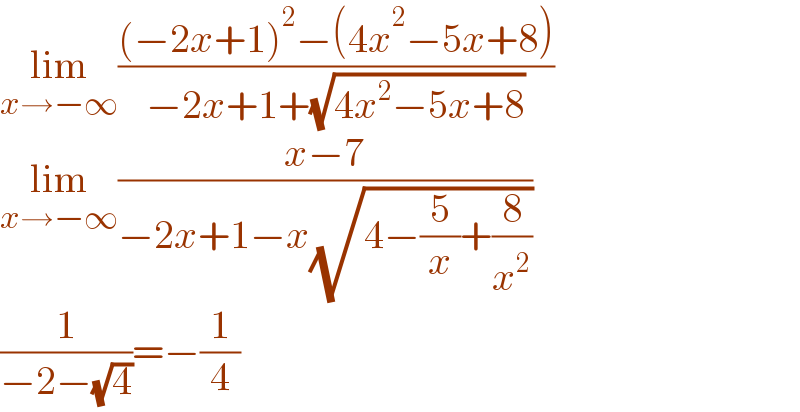
$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{\left(−\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{8}\right)}{−\mathrm{2}{x}+\mathrm{1}+\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{8}}} \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{{x}−\mathrm{7}}{−\mathrm{2}{x}+\mathrm{1}−{x}\sqrt{\mathrm{4}−\frac{\mathrm{5}}{{x}}+\frac{\mathrm{8}}{{x}^{\mathrm{2}} }}} \\ $$$$\frac{\mathrm{1}}{−\mathrm{2}−\sqrt{\mathrm{4}}}=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by mr W last updated on 12/Jul/21

$${correct} \\ $$
Answered by iloveisrael last updated on 13/Jul/21

$$\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left(−\mathrm{2x}+\mathrm{1}−\sqrt{\mathrm{4x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{8}}\right)=? \\ $$$$\mathrm{solution}\::\: \\ $$$$\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left(−\mathrm{2x}+\mathrm{1}−\sqrt{\mathrm{4x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{8}}\:\right) \\ $$$$=\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left(−\mathrm{2x}+\mathrm{1}−\sqrt{\mathrm{4}}\mid\mathrm{x}−\frac{\mathrm{5}}{\mathrm{2}.\mathrm{4}}\mid\right) \\ $$$$=\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left(−\mathrm{2x}+\mathrm{1}−\mathrm{2}\left(−\mathrm{x}+\frac{\mathrm{5}}{\mathrm{8}}\right)\right) \\ $$$$=\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left(−\mathrm{2x}+\mathrm{1}+\mathrm{2x}−\frac{\mathrm{5}}{\mathrm{4}}\right) \\ $$$$=\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{5}}{\mathrm{4}}\right)=−\frac{\mathrm{1}}{\mathrm{4}}.\checkmark \\ $$
