Question Number 146559 by liberty last updated on 14/Jul/21
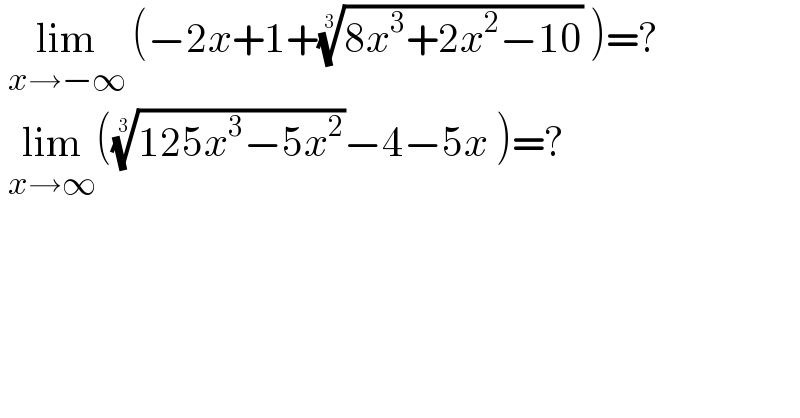
$$\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\left(−\mathrm{2}{x}+\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{8}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{10}}\:\right)=? \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\sqrt[{\mathrm{3}}]{\mathrm{125}{x}^{\mathrm{3}} −\mathrm{5}{x}^{\mathrm{2}} }−\mathrm{4}−\mathrm{5}{x}\:\right)=?\: \\ $$
Answered by iloveisrael last updated on 14/Jul/21
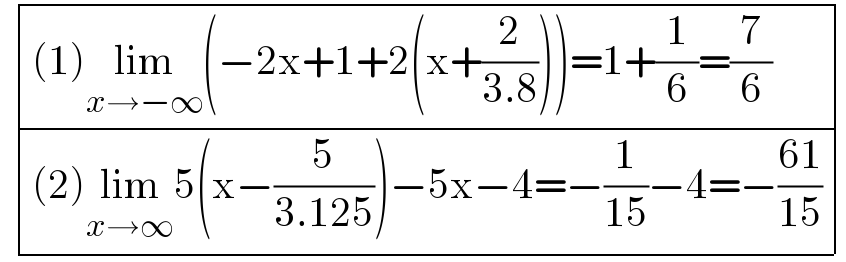
$$\:\begin{array}{|c|c|}{\left(\mathrm{1}\right)\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left(−\mathrm{2x}+\mathrm{1}+\mathrm{2}\left(\mathrm{x}+\frac{\mathrm{2}}{\mathrm{3}.\mathrm{8}}\right)\right)=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{7}}{\mathrm{6}}}\\{\left(\mathrm{2}\right)\underset{{x}\rightarrow\infty} {\mathrm{lim}5}\left(\mathrm{x}−\frac{\mathrm{5}}{\mathrm{3}.\mathrm{125}}\right)−\mathrm{5x}−\mathrm{4}=−\frac{\mathrm{1}}{\mathrm{15}}−\mathrm{4}=−\frac{\mathrm{61}}{\mathrm{15}}}\\\hline\end{array} \\ $$
Answered by liberty last updated on 14/Jul/21
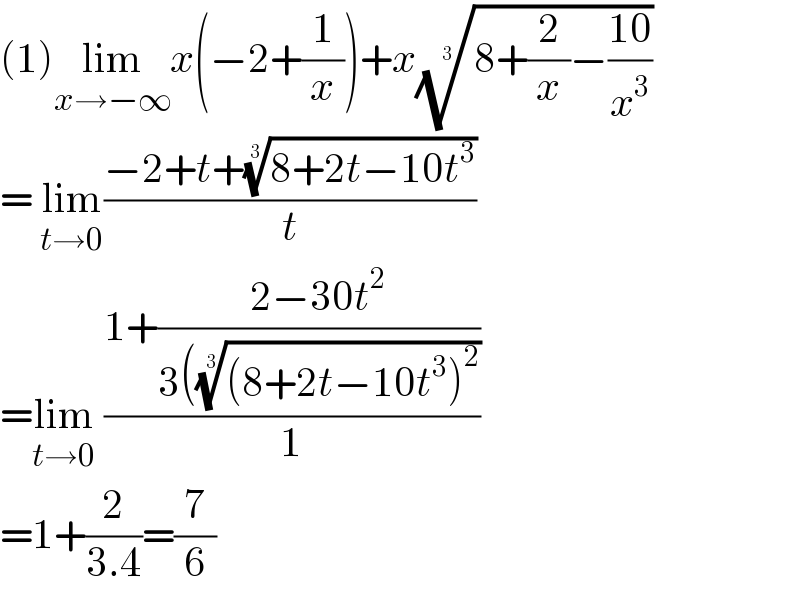
$$\left(\mathrm{1}\right)\underset{{x}\rightarrow−\infty} {\mathrm{lim}}{x}\left(−\mathrm{2}+\frac{\mathrm{1}}{{x}}\right)+{x}\sqrt[{\mathrm{3}}]{\mathrm{8}+\frac{\mathrm{2}}{{x}}−\frac{\mathrm{10}}{{x}^{\mathrm{3}} }}\: \\ $$$$=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}+{t}+\sqrt[{\mathrm{3}}]{\mathrm{8}+\mathrm{2}{t}−\mathrm{10}{t}^{\mathrm{3}} }}{{t}} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}+\frac{\mathrm{2}−\mathrm{30}{t}^{\mathrm{2}} }{\mathrm{3}\left(\sqrt[{\mathrm{3}}]{\left(\mathrm{8}+\mathrm{2}{t}−\mathrm{10}{t}^{\mathrm{3}} \right)^{\mathrm{2}} }\right.}}{\mathrm{1}} \\ $$$$=\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}.\mathrm{4}}=\frac{\mathrm{7}}{\mathrm{6}} \\ $$
