Question Number 120515 by john santu last updated on 01/Nov/20
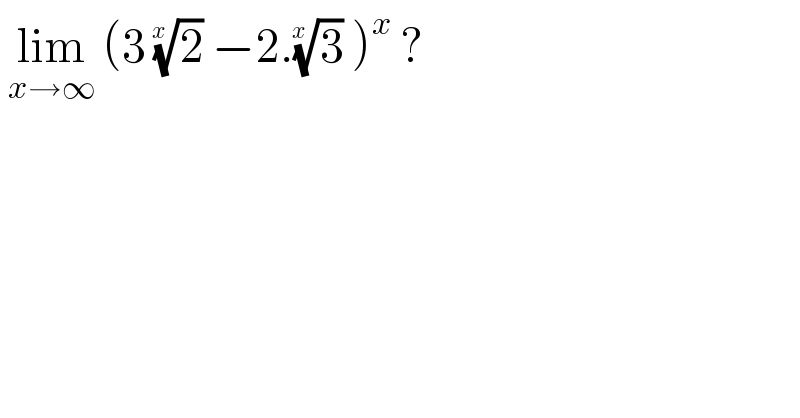
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{3}\:\sqrt[{{x}\:}]{\mathrm{2}}\:−\mathrm{2}.\sqrt[{{x}\:}]{\mathrm{3}}\:\right)^{{x}} \:? \\ $$
Answered by bramlexs22 last updated on 01/Nov/20

$$\mathrm{ln}\:\mathrm{L}\:=\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{x}\:\mathrm{ln}\:\left(\mathrm{3}.\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{x}}} \:−\mathrm{2}.\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{x}}} \:\right) \\ $$$$\mathrm{let}\:\frac{\mathrm{1}}{\mathrm{x}}\:=\:\mathrm{t}\:\wedge\:\mathrm{t}\rightarrow\mathrm{0}^{+} \\ $$$$\mathrm{ln}\:\mathrm{L}\:=\:\underset{\mathrm{t}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\mathrm{3}.\mathrm{2}^{\mathrm{t}} −\mathrm{2}.\mathrm{3}^{\mathrm{t}} \right)}{\mathrm{t}} \\ $$$$\mathrm{ln}\:\mathrm{L}\:=\:\underset{\mathrm{t}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{3}.\mathrm{ln}\:\left(\mathrm{2}\right).\mathrm{2}^{\mathrm{t}} −\mathrm{2}.\mathrm{ln}\:\left(\mathrm{3}\right).\mathrm{3}^{\mathrm{t}} }{\mathrm{3}.\mathrm{2}^{\mathrm{t}} −\mathrm{2}.\mathrm{3}^{\mathrm{t}} } \\ $$$$\mathrm{ln}\:\mathrm{L}\:=\:\mathrm{ln}\:\left(\frac{\mathrm{8}}{\mathrm{9}}\right).\:\mathrm{thus}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{is}\:\mathrm{L}=\mathrm{e}^{\mathrm{ln}\:\left(\frac{\mathrm{8}}{\mathrm{9}}\right)} =\:\frac{\mathrm{8}}{\mathrm{9}} \\ $$
