Question Number 157314 by cortano last updated on 22/Oct/21
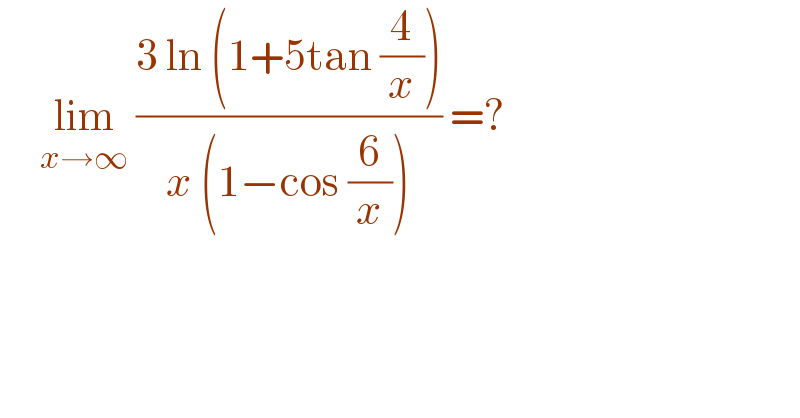
$$\:\:\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}\:\mathrm{ln}\:\left(\mathrm{1}+\mathrm{5tan}\:\frac{\mathrm{4}}{{x}}\right)}{{x}\:\left(\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{6}}{{x}}\right)}\:=? \\ $$
Commented by john_santu last updated on 22/Oct/21
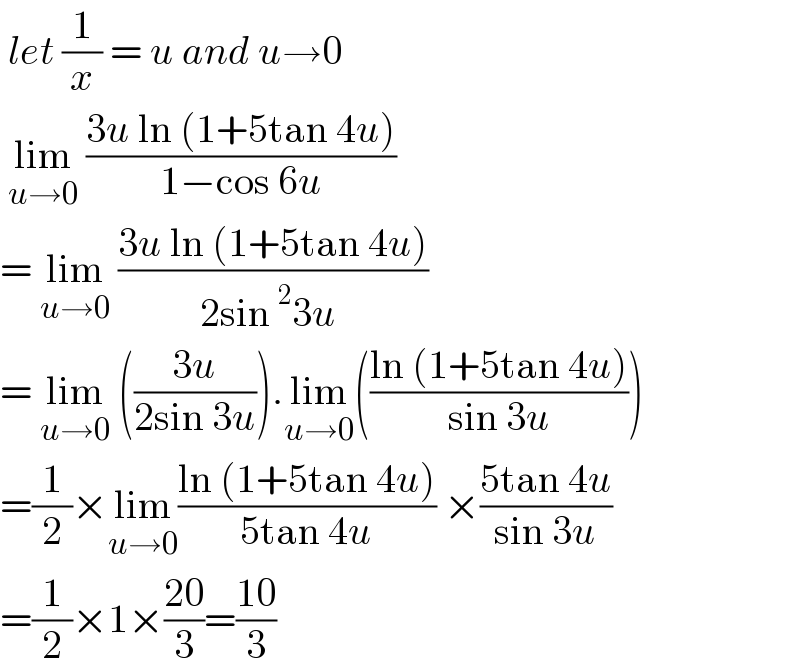
$$\:{let}\:\frac{\mathrm{1}}{{x}}\:=\:{u}\:{and}\:{u}\rightarrow\mathrm{0} \\ $$$$\:\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}{u}\:\mathrm{ln}\:\left(\mathrm{1}+\mathrm{5tan}\:\mathrm{4}{u}\right)}{\mathrm{1}−\mathrm{cos}\:\mathrm{6}{u}} \\ $$$$=\:\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}{u}\:\mathrm{ln}\:\left(\mathrm{1}+\mathrm{5tan}\:\mathrm{4}{u}\right)}{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{3}{u}\:} \\ $$$$=\:\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{3}{u}}{\mathrm{2sin}\:\mathrm{3}{u}}\right).\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{ln}\:\left(\mathrm{1}+\mathrm{5tan}\:\mathrm{4}{u}\right)}{\mathrm{sin}\:\mathrm{3}{u}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\:\left(\mathrm{1}+\mathrm{5tan}\:\mathrm{4}{u}\right)}{\mathrm{5tan}\:\mathrm{4}{u}}\:×\frac{\mathrm{5tan}\:\mathrm{4}{u}}{\mathrm{sin}\:\mathrm{3}{u}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}×\frac{\mathrm{20}}{\mathrm{3}}=\frac{\mathrm{10}}{\mathrm{3}} \\ $$
