Menu Close

lim-x-3-sin-x-sin-3-1-x-3-

Tinku Tara 0 Comments
Pin




Question Number 81096 by jagoll last updated on 09/Feb/20
lim_(x→3) (((sin x)/(sin 3)))^(1/(x−3)) =?
$$\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\left(\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:\mathrm{3}}\right)^{\frac{\mathrm{1}}{{x}−\mathrm{3}}} \:=? \\ $$
Commented by abdomathmax last updated on 09/Feb/20
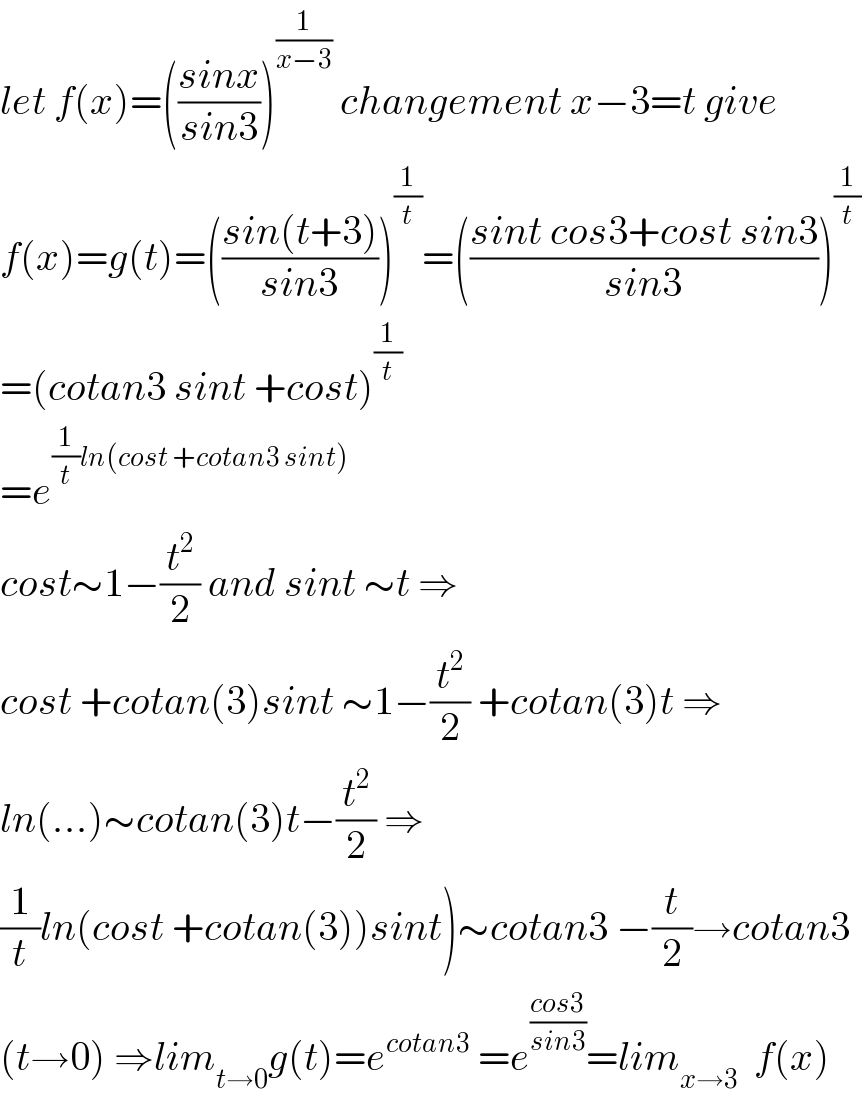
let f(x)=(((sinx)/(sin3)))^(1/(x−3)) changement x−3=t give f(x)=g(t)=(((sin(t+3))/(sin3)))^(1/t) =(((sint cos3+cost sin3)/(sin3)))^(1/t) =(cotan3 sint +cost)^(1/t) =e^((1/t)ln(cost +cotan3 sint)) cost∼1−(t^2 /2) and sint ∼t ⇒ cost +cotan(3)sint ∼1−(t^2 /2) +cotan(3)t ⇒ ln(...)∼cotan(3)t−(t^2 /2) ⇒ (1/t)ln(cost +cotan(3))sint)∼cotan3 −(t/2)→cotan3 (t→0) ⇒lim_(t→0) g(t)=e^(cotan3) =e^((cos3)/(sin3)) =lim_(x→3) f(x)
$${let}\:{f}\left({x}\right)=\left(\frac{{sinx}}{{sin}\mathrm{3}}\right)^{\frac{\mathrm{1}}{{x}−\mathrm{3}}} \:{changement}\:{x}−\mathrm{3}={t}\:{give} \\ $$$${f}\left({x}\right)={g}\left({t}\right)=\left(\frac{{sin}\left({t}+\mathrm{3}\right)}{{sin}\mathrm{3}}\right)^{\frac{\mathrm{1}}{{t}}} =\left(\frac{{sint}\:{cos}\mathrm{3}+{cost}\:{sin}\mathrm{3}}{{sin}\mathrm{3}}\right)^{\frac{\mathrm{1}}{{t}}} \\ $$$$=\left({cotan}\mathrm{3}\:{sint}\:+{cost}\right)^{\frac{\mathrm{1}}{{t}}} \\ $$$$={e}^{\frac{\mathrm{1}}{{t}}{ln}\left({cost}\:+{cotan}\mathrm{3}\:{sint}\right)} \\ $$$${cost}\sim\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:{and}\:{sint}\:\sim{t}\:\Rightarrow \\ $$$${cost}\:+{cotan}\left(\mathrm{3}\right){sint}\:\sim\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:+{cotan}\left(\mathrm{3}\right){t}\:\Rightarrow \\ $$$${ln}\left(…\right)\sim{cotan}\left(\mathrm{3}\right){t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\left.\frac{\mathrm{1}}{{t}}{ln}\left({cost}\:+{cotan}\left(\mathrm{3}\right)\right){sint}\right)\sim{cotan}\mathrm{3}\:−\frac{{t}}{\mathrm{2}}\rightarrow{cotan}\mathrm{3} \\ $$$$\left({t}\rightarrow\mathrm{0}\right)\:\Rightarrow{lim}_{{t}\rightarrow\mathrm{0}} {g}\left({t}\right)={e}^{{cotan}\mathrm{3}} \:={e}^{\frac{{cos}\mathrm{3}}{{sin}\mathrm{3}}} ={lim}_{{x}\rightarrow\mathrm{3}} \:\:{f}\left({x}\right) \\ $$
Answered by john santu last updated on 09/Feb/20
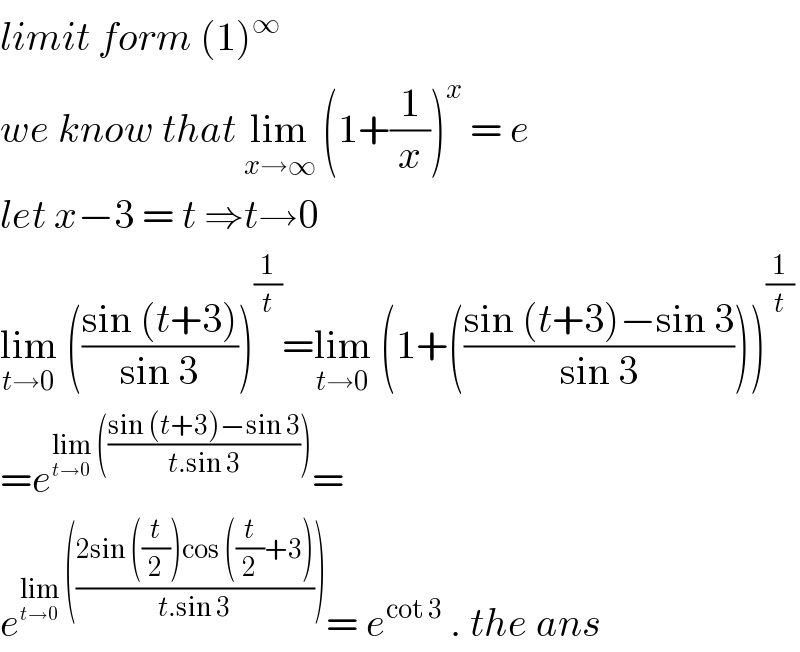
limit form (1)^∞ we know that lim_(x→∞) (1+(1/x))^x = e let x−3 = t ⇒t→0 lim_(t→0) (((sin (t+3))/(sin 3)))^(1/t) =lim_(t→0) (1+(((sin (t+3)−sin 3)/(sin 3))))^(1/t) =e^(lim_(t→0) (((sin (t+3)−sin 3)/(t.sin 3)))) = e^(lim_(t→0) (((2sin ((t/2))cos ((t/2)+3))/(t.sin 3)))) = e^(cot 3) . the ans
$${limit}\:{form}\:\left(\mathrm{1}\right)^{\infty} \\ $$$${we}\:{know}\:{that}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} \:=\:{e} \\ $$$${let}\:{x}−\mathrm{3}\:=\:{t}\:\Rightarrow{t}\rightarrow\mathrm{0} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{sin}\:\left({t}+\mathrm{3}\right)}{\mathrm{sin}\:\mathrm{3}}\right)^{\frac{\mathrm{1}}{{t}}} =\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{1}+\left(\frac{\mathrm{sin}\:\left({t}+\mathrm{3}\right)−\mathrm{sin}\:\mathrm{3}}{\mathrm{sin}\:\mathrm{3}}\right)\right)^{\frac{\mathrm{1}}{{t}}} \\ $$$$={e}^{\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{sin}\:\left({t}+\mathrm{3}\right)−\mathrm{sin}\:\mathrm{3}}{{t}.\mathrm{sin}\:\mathrm{3}}\right)} = \\ $$$${e}^{\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{2sin}\:\left(\frac{{t}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{t}}{\mathrm{2}}+\mathrm{3}\right)}{{t}.\mathrm{sin}\:\mathrm{3}}\right)} =\:{e}^{\mathrm{cot}\:\mathrm{3}} \:.\:{the}\:{ans} \\ $$
Commented by jagoll last updated on 09/Feb/20
waw thank you sir
$${waw}\:{thank}\:{you}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *