Question Number 160865 by vvvv last updated on 08/Dec/21

$$\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{3}} {\boldsymbol{\mathrm{lim}}}\frac{\boldsymbol{{tan}}\left(\boldsymbol{{x}}\right)−\boldsymbol{{tan}}\left(\mathrm{3}\right)}{\boldsymbol{{sin}}\left(\boldsymbol{{ln}}\left(\boldsymbol{{x}}−\mathrm{2}\right)\right)} \\ $$$$\boldsymbol{{work}}\:\boldsymbol{{with}}\:{the}\:{rule}\:{of} \\ $$$${substitution}\:\:{of}\:{infinitely} \\ $$$${small}\:\:{functions}\:{equivalent}\: \\ $$$${to}\:{a}\:{limit} \\ $$
Commented by cortano last updated on 08/Dec/21
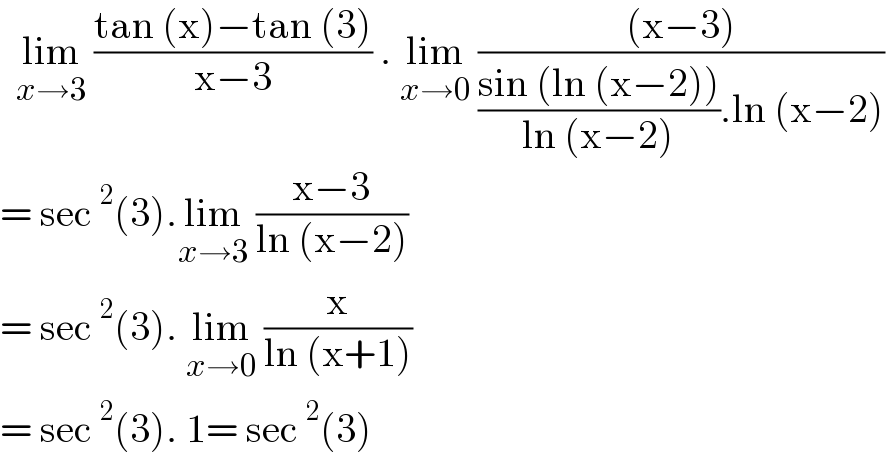
$$\:\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left(\mathrm{x}\right)−\mathrm{tan}\:\left(\mathrm{3}\right)}{\mathrm{x}−\mathrm{3}}\:.\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{x}−\mathrm{3}\right)}{\frac{\mathrm{sin}\:\left(\mathrm{ln}\:\left(\mathrm{x}−\mathrm{2}\right)\right)}{\mathrm{ln}\:\left(\mathrm{x}−\mathrm{2}\right)}.\mathrm{ln}\:\left(\mathrm{x}−\mathrm{2}\right)} \\ $$$$=\:\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{3}\right).\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\mathrm{x}−\mathrm{3}}{\mathrm{ln}\:\left(\mathrm{x}−\mathrm{2}\right)}\: \\ $$$$=\:\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{3}\right).\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}}{\mathrm{ln}\:\left(\mathrm{x}+\mathrm{1}\right)} \\ $$$$=\:\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{3}\right).\:\mathrm{1}=\:\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{3}\right) \\ $$
