Menu Close

lim-x-3-x-2-7-25-x-2-8-3x-6-18-3x-

Tinku Tara 0 Comments
Pin




Question Number 169635 by cortano1 last updated on 05/May/22
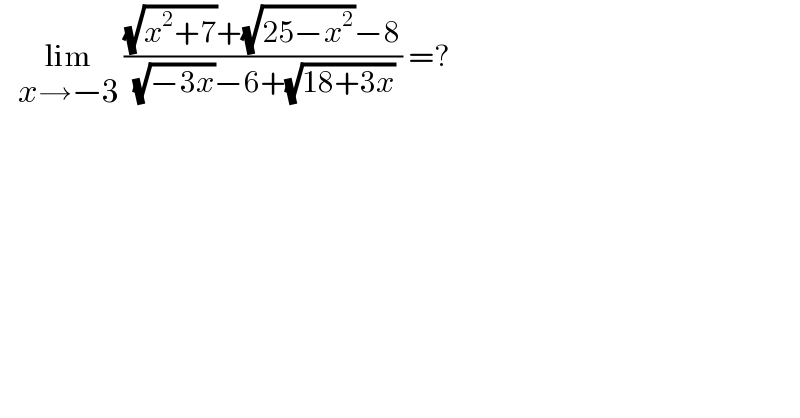
lim_(x→−3) (((√(x^2 +7))+(√(25−x^2 ))−8)/( (√(−3x))−6+(√(18+3x)))) =?
$$\:\:\:\underset{{x}\rightarrow−\mathrm{3}} {\mathrm{lim}}\:\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}+\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }−\mathrm{8}}{\:\sqrt{−\mathrm{3}{x}}−\mathrm{6}+\sqrt{\mathrm{18}+\mathrm{3}{x}}}\:=? \\ $$
Commented by cortano1 last updated on 05/May/22
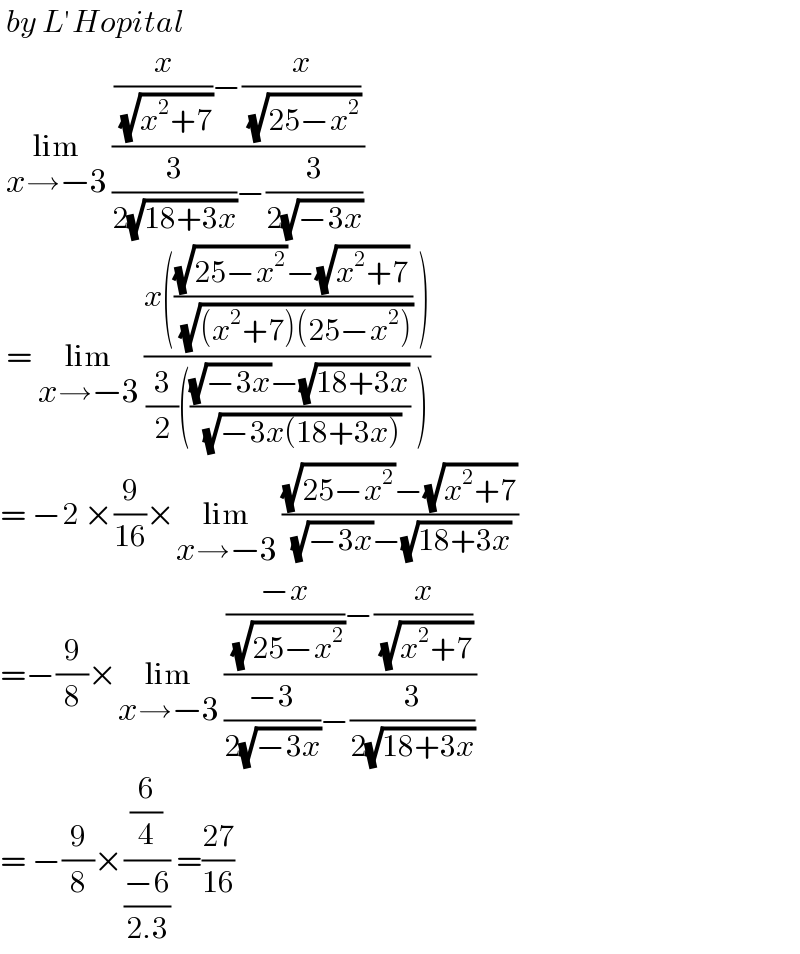
by L′Hopital lim_(x→−3) (((x/( (√(x^2 +7))))−(x/( (√(25−x^2 )))))/((3/(2(√(18+3x))))−(3/(2(√(−3x)))))) = lim_(x→−3) ((x((((√(25−x^2 ))−(√(x^2 +7)))/( (√((x^2 +7)(25−x^2 ))))) ))/((3/2)((((√(−3x))−(√(18+3x)))/( (√(−3x(18+3x))))) ))) = −2 ×(9/(16))×lim_(x→−3) (((√(25−x^2 ))−(√(x^2 +7)))/( (√(−3x))−(√(18+3x)))) =−(9/8)×lim_(x→−3) ((((−x)/( (√(25−x^2 ))))−(x/( (√(x^2 +7)))))/(((−3)/(2(√(−3x))))−(3/(2(√(18+3x)))))) = −(9/8)×((6/4)/((−6)/(2.3))) =((27)/(16))
$$\:{by}\:{L}'{Hopital} \\ $$$$\:\underset{{x}\rightarrow−\mathrm{3}} {\mathrm{lim}}\:\frac{\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}}−\frac{{x}}{\:\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }}}{\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{18}+\mathrm{3}{x}}}−\frac{\mathrm{3}}{\mathrm{2}\sqrt{−\mathrm{3}{x}}}}\: \\ $$$$\:=\:\underset{{x}\rightarrow−\mathrm{3}} {\mathrm{lim}}\:\frac{{x}\left(\frac{\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }−\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}}{\:\sqrt{\left({x}^{\mathrm{2}} +\mathrm{7}\right)\left(\mathrm{25}−{x}^{\mathrm{2}} \right)}}\:\right)}{\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\sqrt{−\mathrm{3}{x}}−\sqrt{\mathrm{18}+\mathrm{3}{x}}}{\:\sqrt{−\mathrm{3}{x}\left(\mathrm{18}+\mathrm{3}{x}\right)}}\:\right)} \\ $$$$=\:−\mathrm{2}\:×\frac{\mathrm{9}}{\mathrm{16}}×\underset{{x}\rightarrow−\mathrm{3}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }−\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}}{\:\sqrt{−\mathrm{3}{x}}−\sqrt{\mathrm{18}+\mathrm{3}{x}}} \\ $$$$=−\frac{\mathrm{9}}{\mathrm{8}}×\underset{{x}\rightarrow−\mathrm{3}} {\mathrm{lim}}\:\frac{\frac{−{x}}{\:\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }}−\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}}}{\frac{−\mathrm{3}}{\mathrm{2}\sqrt{−\mathrm{3}{x}}}−\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{18}+\mathrm{3}{x}}}} \\ $$$$=\:−\frac{\mathrm{9}}{\mathrm{8}}×\frac{\frac{\mathrm{6}}{\mathrm{4}}}{\frac{−\mathrm{6}}{\mathrm{2}.\mathrm{3}}}\:=\frac{\mathrm{27}}{\mathrm{16}} \\ $$
Answered by bobhans last updated on 05/May/22
lim_(x+3→0) (((√(x^2 +7))−4+(√(25−x^2 ))−4)/( (√(−3x))−3 + (√(18+3x))−3)) = lim_(x+3→0) (((((x−3)(x+3))/( (√(x^2 +7))+4)) −(((x−3)(x+3))/( (√(25−x^2 )) +4)))/(((−3(x+3))/( (√(−3x))+3)) +((3(x+3))/( (√(18+3x))+3)))) = lim_(x+3→0) (((x+3)(x−3)((((√(25−x^2 ))−(√(x^2 +7)))/(((√(x^2 +7))+4)((√(18+3x))+4)))))/(3(x+3)((((√(−3x))−(√(18+3x)))/(((√(−3x))+3)((√(18+3x))+3))))) = −2×((36)/(64)) ×lim_(x+3→0) (((√(25−x^2 ))−(√(x^2 +7)))/( (√(−3x))−(√(18+3x)))) = −(9/8) ×lim_(x+3→0) ((18−2x^2 )/(−6x−18)) . (((√(−3x))+(√(18+3x)))/( (√(25−x^2 ))+(√(x^2 +7)))) = −(9/8)×(6/8)×lim_(x+3→0) ((2(3−x)(3+x))/(−6(x+3))) =−((27)/(32))×((2(6))/(−6)) = ((27)/(16))
$$\:\:\underset{{x}+\mathrm{3}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}−\mathrm{4}+\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }−\mathrm{4}}{\:\sqrt{−\mathrm{3}{x}}−\mathrm{3}\:+\:\sqrt{\mathrm{18}+\mathrm{3}{x}}−\mathrm{3}} \\ $$$$\:=\:\underset{{x}+\mathrm{3}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\left({x}−\mathrm{3}\right)\left({x}+\mathrm{3}\right)}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}+\mathrm{4}}\:−\frac{\left({x}−\mathrm{3}\right)\left({x}+\mathrm{3}\right)}{\:\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }\:+\mathrm{4}}}{\frac{−\mathrm{3}\left({x}+\mathrm{3}\right)}{\:\sqrt{−\mathrm{3}{x}}+\mathrm{3}}\:+\frac{\mathrm{3}\left({x}+\mathrm{3}\right)}{\:\sqrt{\mathrm{18}+\mathrm{3}{x}}+\mathrm{3}}} \\ $$$$\:=\:\underset{{x}+\mathrm{3}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\cancel{\left({x}+\mathrm{3}\right)}\left({x}−\mathrm{3}\right)\left(\frac{\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }−\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}}{\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}+\mathrm{4}\right)\left(\sqrt{\mathrm{18}+\mathrm{3}{x}}+\mathrm{4}\right)}\right)}{\mathrm{3}\cancel{\left({x}+\mathrm{3}\right)}\left(\frac{\sqrt{−\mathrm{3}{x}}−\sqrt{\mathrm{18}+\mathrm{3}{x}}}{\left(\sqrt{−\mathrm{3}{x}}+\mathrm{3}\right)\left(\sqrt{\mathrm{18}+\mathrm{3}{x}}+\mathrm{3}\right.}\right)} \\ $$$$=\:−\mathrm{2}×\frac{\mathrm{36}}{\mathrm{64}}\:×\underset{{x}+\mathrm{3}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }−\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}}{\:\sqrt{−\mathrm{3}{x}}−\sqrt{\mathrm{18}+\mathrm{3}{x}}} \\ $$$$=\:−\frac{\mathrm{9}}{\mathrm{8}}\:×\underset{{x}+\mathrm{3}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{18}−\mathrm{2}{x}^{\mathrm{2}} }{−\mathrm{6}{x}−\mathrm{18}}\:.\:\frac{\sqrt{−\mathrm{3}{x}}+\sqrt{\mathrm{18}+\mathrm{3}{x}}}{\:\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }+\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}} \\ $$$$=\:−\frac{\mathrm{9}}{\mathrm{8}}×\frac{\mathrm{6}}{\mathrm{8}}×\underset{{x}+\mathrm{3}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\left(\mathrm{3}−{x}\right)\cancel{\left(\mathrm{3}+{x}\right)}}{−\mathrm{6}\cancel{\left({x}+\mathrm{3}\right)}}\: \\ $$$$=−\frac{\mathrm{27}}{\mathrm{32}}×\frac{\mathrm{2}\left(\mathrm{6}\right)}{−\mathrm{6}}\:=\:\frac{\mathrm{27}}{\mathrm{16}}\: \\ $$
Commented by Rasheed.Sindhi last updated on 05/May/22
Nice!
$$\mathcal{N}{ice}! \\ $$
Commented by mathlove last updated on 06/May/22
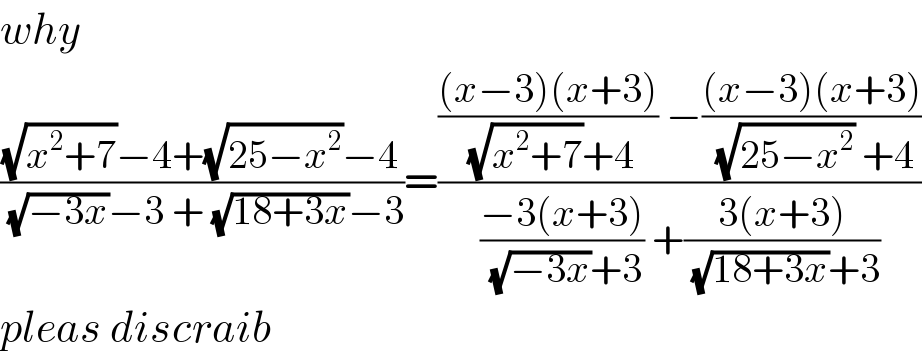
why (((√(x^2 +7))−4+(√(25−x^2 ))−4)/( (√(−3x))−3 + (√(18+3x))−3))=(((((x−3)(x+3))/( (√(x^2 +7))+4)) −(((x−3)(x+3))/( (√(25−x^2 )) +4)))/(((−3(x+3))/( (√(−3x))+3)) +((3(x+3))/( (√(18+3x))+3)))) pleas discraib
$${why} \\ $$$$\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}−\mathrm{4}+\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }−\mathrm{4}}{\:\sqrt{−\mathrm{3}{x}}−\mathrm{3}\:+\:\sqrt{\mathrm{18}+\mathrm{3}{x}}−\mathrm{3}}=\frac{\frac{\left({x}−\mathrm{3}\right)\left({x}+\mathrm{3}\right)}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}+\mathrm{4}}\:−\frac{\left({x}−\mathrm{3}\right)\left({x}+\mathrm{3}\right)}{\:\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }\:+\mathrm{4}}}{\frac{−\mathrm{3}\left({x}+\mathrm{3}\right)}{\:\sqrt{−\mathrm{3}{x}}+\mathrm{3}}\:+\frac{\mathrm{3}\left({x}+\mathrm{3}\right)}{\:\sqrt{\mathrm{18}+\mathrm{3}{x}}+\mathrm{3}}} \\ $$$${pleas}\:{discraib} \\ $$
Commented by Rasheed.Sindhi last updated on 06/May/22
(((√(x^2 +7))−4+(√(25−x^2 ))−4)/( (√(−3x))−3 + (√(18+3x))−3)) =((((((√(x^2 +7))−4)((√(x^2 +7))+4))/( (√(x^2 +7))+4))+((((√(25−x^2 ))−4)((√(25−x^2 )) +4))/( (√(25−x^2 ))+4)))/(((((√(−3x))−3)((√(−3x))+3))/( (√(−3x))+3))+((( (√(18+3x))−3)( (√(18+3x))+3))/( (√(18+3x))+3)))) =((((((√(x^2 +7)))^2 −(4)^2 )/( (√(x^2 +7))+4))+((((√(25−x^2 )))^2 −(4)^2 )/( (√(25−x^2 ))+4)))/(((((√(−3x)))^2 −(3)^2 )/( (√(−3x))+3))+((( (√(18+3x)))^2 −(3)^2 )/( (√(18+3x))+3)))) =((((x^2 +7−16)/( (√(x^2 +7))+4))+((25−x^2 −16)/( (√(25−x^2 ))+4)))/(((−3x−9)/( (√(−3x))+3))+(( 18+3x−9)/( (√(18+3x))+3)))) =((((x^2 −9)/( (√(x^2 +7))+4))+((9−x^2 )/( (√(25−x^2 ))+4)))/(((−3x−9)/( (√(−3x))+3))+(( 3x+9)/( (√(18+3x))+3)))) =(((((x−3)(x+3))/( (√(x^2 +7))+4))−(((x−3)(x+3))/( (√(25−x^2 ))+4)))/(((−3x−9)/( (√(−3x))+3))+(( 3x+9)/( (√(18+3x))+3)))) =(((((x−3)(x+3))/( (√(x^2 +7))+4))−(((x−3)(x+3))/( (√(25−x^2 ))+4)))/(((−3(x+3))/( (√(−3x))+3))+(( 3(x+3))/( (√(18+3x))+3))))
$$\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}−\mathrm{4}+\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }−\mathrm{4}}{\:\sqrt{−\mathrm{3}{x}}−\mathrm{3}\:+\:\sqrt{\mathrm{18}+\mathrm{3}{x}}−\mathrm{3}} \\ $$$$=\frac{\frac{\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}−\mathrm{4}\right)\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}+\mathrm{4}\right)}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}+\mathrm{4}}+\frac{\left(\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }−\mathrm{4}\right)\left(\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }\:+\mathrm{4}\right)}{\:\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }+\mathrm{4}}}{\frac{\left(\sqrt{−\mathrm{3}{x}}−\mathrm{3}\right)\left(\sqrt{−\mathrm{3}{x}}+\mathrm{3}\right)}{\:\sqrt{−\mathrm{3}{x}}+\mathrm{3}}+\frac{\left(\:\sqrt{\mathrm{18}+\mathrm{3}{x}}−\mathrm{3}\right)\left(\:\sqrt{\mathrm{18}+\mathrm{3}{x}}+\mathrm{3}\right)}{\:\sqrt{\mathrm{18}+\mathrm{3}{x}}+\mathrm{3}}} \\ $$$$=\frac{\frac{\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}\right)^{\mathrm{2}} −\left(\mathrm{4}\right)^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}+\mathrm{4}}+\frac{\left(\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }\right)^{\mathrm{2}} −\left(\mathrm{4}\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }+\mathrm{4}}}{\frac{\left(\sqrt{−\mathrm{3}{x}}\right)^{\mathrm{2}} −\left(\mathrm{3}\right)^{\mathrm{2}} }{\:\sqrt{−\mathrm{3}{x}}+\mathrm{3}}+\frac{\left(\:\sqrt{\mathrm{18}+\mathrm{3}{x}}\right)^{\mathrm{2}} −\left(\mathrm{3}\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{18}+\mathrm{3}{x}}+\mathrm{3}}} \\ $$$$=\frac{\frac{{x}^{\mathrm{2}} +\mathrm{7}−\mathrm{16}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}+\mathrm{4}}+\frac{\mathrm{25}−{x}^{\mathrm{2}} −\mathrm{16}}{\:\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }+\mathrm{4}}}{\frac{−\mathrm{3}{x}−\mathrm{9}}{\:\sqrt{−\mathrm{3}{x}}+\mathrm{3}}+\frac{\:\mathrm{18}+\mathrm{3}{x}−\mathrm{9}}{\:\sqrt{\mathrm{18}+\mathrm{3}{x}}+\mathrm{3}}} \\ $$$$=\frac{\frac{{x}^{\mathrm{2}} −\mathrm{9}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}+\mathrm{4}}+\frac{\mathrm{9}−{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }+\mathrm{4}}}{\frac{−\mathrm{3}{x}−\mathrm{9}}{\:\sqrt{−\mathrm{3}{x}}+\mathrm{3}}+\frac{\:\mathrm{3}{x}+\mathrm{9}}{\:\sqrt{\mathrm{18}+\mathrm{3}{x}}+\mathrm{3}}} \\ $$$$=\frac{\frac{\left({x}−\mathrm{3}\right)\left({x}+\mathrm{3}\right)}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}+\mathrm{4}}−\frac{\left({x}−\mathrm{3}\right)\left({x}+\mathrm{3}\right)}{\:\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }+\mathrm{4}}}{\frac{−\mathrm{3}{x}−\mathrm{9}}{\:\sqrt{−\mathrm{3}{x}}+\mathrm{3}}+\frac{\:\mathrm{3}{x}+\mathrm{9}}{\:\sqrt{\mathrm{18}+\mathrm{3}{x}}+\mathrm{3}}} \\ $$$$=\frac{\frac{\left({x}−\mathrm{3}\right)\left({x}+\mathrm{3}\right)}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{7}}+\mathrm{4}}−\frac{\left({x}−\mathrm{3}\right)\left({x}+\mathrm{3}\right)}{\:\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }+\mathrm{4}}}{\frac{−\mathrm{3}\left({x}+\mathrm{3}\right)}{\:\sqrt{−\mathrm{3}{x}}+\mathrm{3}}+\frac{\:\mathrm{3}\left({x}+\mathrm{3}\right)}{\:\sqrt{\mathrm{18}+\mathrm{3}{x}}+\mathrm{3}}} \\ $$
Commented by mathlove last updated on 06/May/22
thanks dear
$${thanks}\:{dear} \\ $$
Commented by otchereabdullai@gmail.com last updated on 06/May/22
nice!
$$\mathrm{nice}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *