Menu Close

lim-x-3-x-3-x-1-3-5-x-1-5-2x-3-3x-2-1-3-

Tinku Tara 0 Comments
Pin




Question Number 122338 by benjo_mathlover last updated on 15/Nov/20
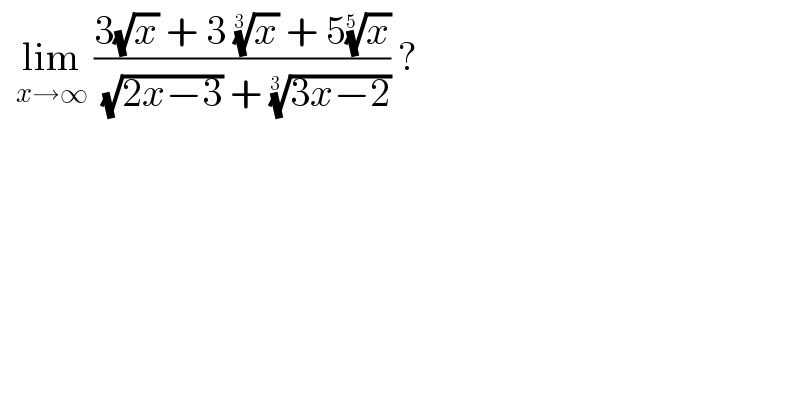
lim_(x→∞) ((3(√x) + 3 (x)^(1/(3 )) + 5(x)^(1/(5 )) )/( (√(2x−3)) + ((3x−2))^(1/(3 )) )) ?
$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}\sqrt{{x}}\:+\:\mathrm{3}\:\sqrt[{\mathrm{3}\:}]{{x}}\:+\:\mathrm{5}\sqrt[{\mathrm{5}\:}]{{x}}}{\:\sqrt{\mathrm{2}{x}−\mathrm{3}}\:+\:\sqrt[{\mathrm{3}\:}]{\mathrm{3}{x}−\mathrm{2}}}\:?\: \\ $$
Commented by liberty last updated on 16/Nov/20
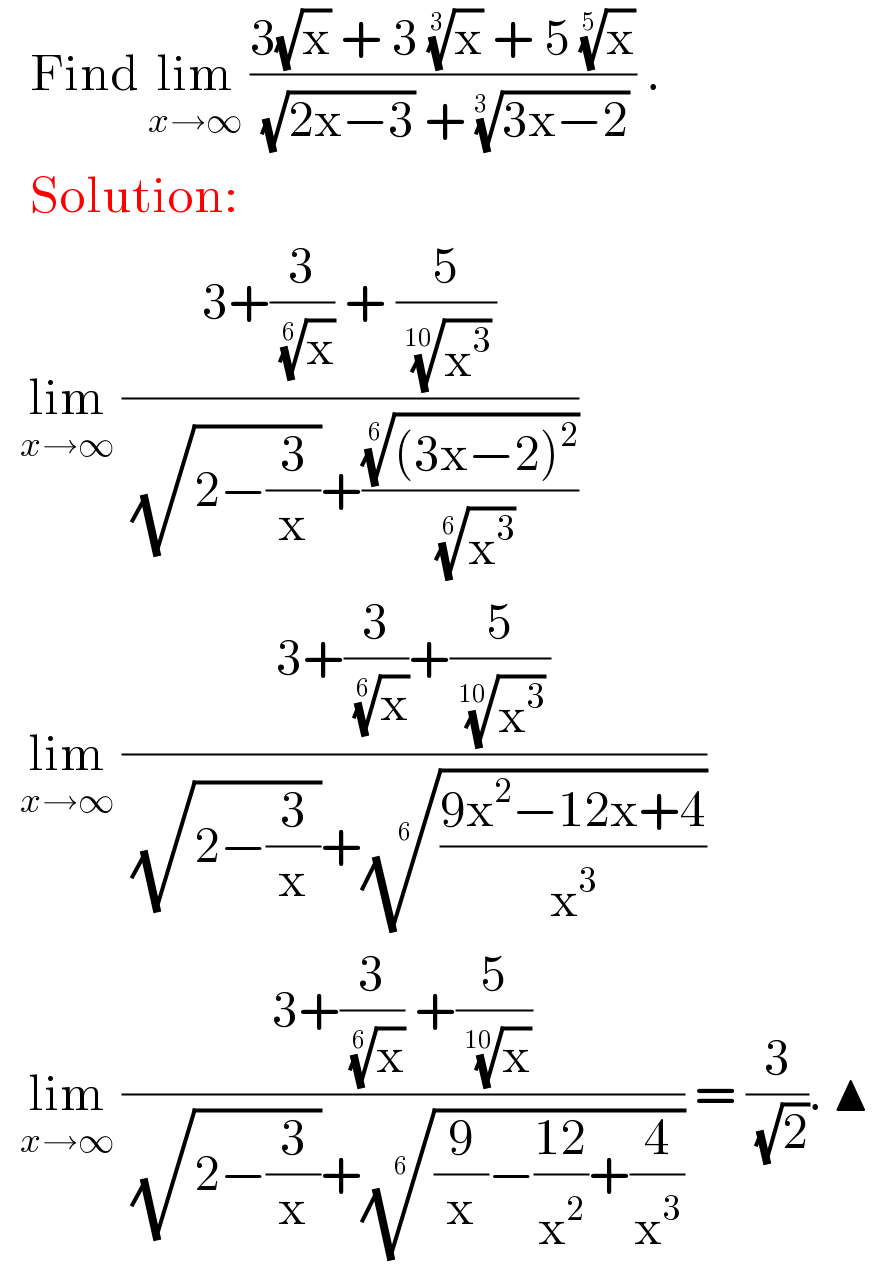
Find lim_(x→∞) ((3(√x) + 3 (x)^(1/3) + 5 (x)^(1/5) )/( (√(2x−3)) + ((3x−2))^(1/(3 )) )) . Solution: lim_(x→∞) ((3+(3/( (x)^(1/6) )) + (5/( (x^3 )^(1/(10)) )))/( (√(2−(3/x)))+((((3x−2)^2 ))^(1/6) /( (x^3 )^(1/6) )))) lim_(x→∞) ((3+(3/( (x)^(1/6) ))+(5/( (x^3 )^(1/(10)) )))/( (√(2−(3/x)))+(((9x^2 −12x+4)/x^3 ))^(1/6) )) lim_(x→∞) ((3+(3/( (x)^(1/6) )) +(5/( (x)^(1/(10)) )))/( (√(2−(3/x)))+(((9/x)−((12)/x^2 )+(4/x^3 )))^(1/6) )) = (3/( (√2))). ▲
$$\:\:\:\mathrm{Find}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}\sqrt{\mathrm{x}}\:+\:\mathrm{3}\:\sqrt[{\mathrm{3}}]{\mathrm{x}}\:+\:\mathrm{5}\:\sqrt[{\mathrm{5}}]{\mathrm{x}}}{\:\sqrt{\mathrm{2x}−\mathrm{3}}\:+\:\sqrt[{\mathrm{3}\:}]{\mathrm{3x}−\mathrm{2}}}\:. \\ $$$$\:\:\:\mathrm{Solution}: \\ $$$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}+\frac{\mathrm{3}}{\:\sqrt[{\mathrm{6}}]{\mathrm{x}}}\:+\:\frac{\mathrm{5}}{\:\sqrt[{\mathrm{10}}]{\mathrm{x}^{\mathrm{3}} }}}{\:\sqrt{\mathrm{2}−\frac{\mathrm{3}}{\mathrm{x}}}+\frac{\sqrt[{\mathrm{6}}]{\left(\mathrm{3x}−\mathrm{2}\right)^{\mathrm{2}} }}{\:\sqrt[{\mathrm{6}}]{\mathrm{x}^{\mathrm{3}} }}} \\ $$$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}+\frac{\mathrm{3}}{\:\sqrt[{\mathrm{6}}]{\mathrm{x}}}+\frac{\mathrm{5}}{\:\sqrt[{\mathrm{10}}]{\mathrm{x}^{\mathrm{3}} }}}{\:\sqrt{\mathrm{2}−\frac{\mathrm{3}}{\mathrm{x}}}+\sqrt[{\mathrm{6}}]{\frac{\mathrm{9x}^{\mathrm{2}} −\mathrm{12x}+\mathrm{4}}{\mathrm{x}^{\mathrm{3}} }}} \\ $$$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}+\frac{\mathrm{3}}{\:\sqrt[{\mathrm{6}}]{\mathrm{x}}}\:+\frac{\mathrm{5}}{\:\sqrt[{\mathrm{10}}]{\mathrm{x}}}}{\:\sqrt{\mathrm{2}−\frac{\mathrm{3}}{\mathrm{x}}}+\sqrt[{\mathrm{6}}]{\frac{\mathrm{9}}{\mathrm{x}}−\frac{\mathrm{12}}{\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{3}} }}}\:=\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}.\:\blacktriangle \\ $$
Commented by benjo_mathlover last updated on 16/Nov/20
yes...thanks
$${yes}…{thanks} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *