Question Number 120843 by bramlexs22 last updated on 03/Nov/20

$$\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{x}+\mathrm{9}−\mathrm{6}\sqrt{\mathrm{x}}}}{\:\sqrt{\mathrm{x}}−\mathrm{3}}\:? \\ $$
Commented by Dwaipayan Shikari last updated on 03/Nov/20

$$\frac{\sqrt{\mathrm{12}−\mathrm{6}\sqrt{\mathrm{3}}}}{\:\sqrt{\mathrm{3}}−\mathrm{3}}=−\mathrm{1} \\ $$
Answered by Jamshidbek2311 last updated on 03/Nov/20
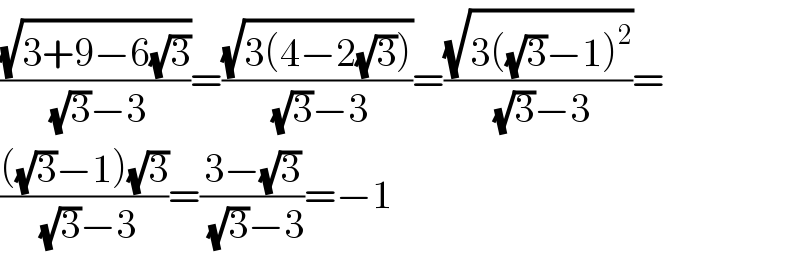
$$\frac{\sqrt{\mathrm{3}+\mathrm{9}−\mathrm{6}\sqrt{\mathrm{3}}}}{\:\sqrt{\mathrm{3}}−\mathrm{3}}=\frac{\sqrt{\mathrm{3}\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\right)}}{\:\sqrt{\mathrm{3}}−\mathrm{3}}=\frac{\sqrt{\mathrm{3}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} }}{\:\sqrt{\mathrm{3}}−\mathrm{3}}= \\ $$$$\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{3}}−\mathrm{3}}=\frac{\mathrm{3}−\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{3}}−\mathrm{3}}=−\mathrm{1} \\ $$
