Question Number 115775 by bemath last updated on 28/Sep/20
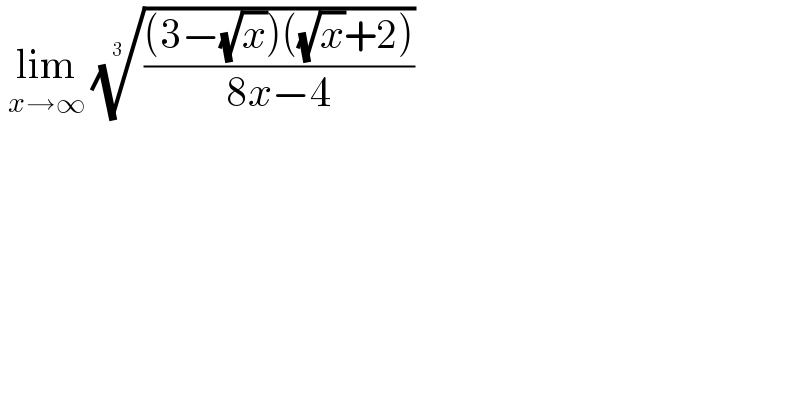
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{3}\:}]{\frac{\left(\mathrm{3}−\sqrt{{x}}\right)\left(\sqrt{{x}}+\mathrm{2}\right)}{\mathrm{8}{x}−\mathrm{4}}} \\ $$
Answered by bobhans last updated on 28/Sep/20
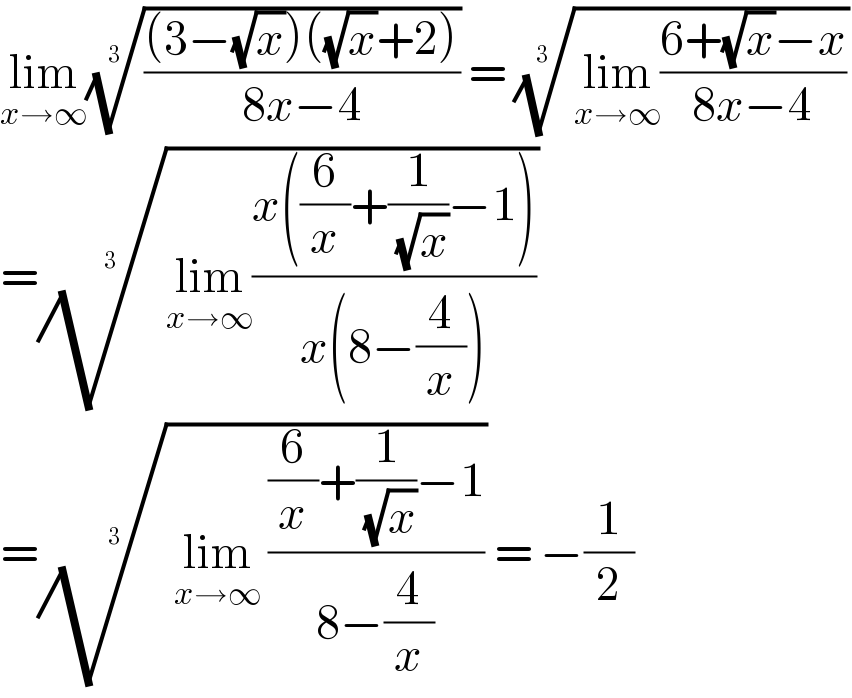
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt[{\mathrm{3}\:}]{\frac{\left(\mathrm{3}−\sqrt{{x}}\right)\left(\sqrt{{x}}+\mathrm{2}\right)}{\mathrm{8}{x}−\mathrm{4}}}\:=\:\sqrt[{\mathrm{3}\:}]{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{6}+\sqrt{{x}}−{x}}{\mathrm{8}{x}−\mathrm{4}}} \\ $$$$=\sqrt[{\mathrm{3}\:}]{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{x}\left(\frac{\mathrm{6}}{{x}}+\frac{\mathrm{1}}{\:\sqrt{{x}}}−\mathrm{1}\right)}{{x}\left(\mathrm{8}−\frac{\mathrm{4}}{{x}}\right)}} \\ $$$$=\sqrt[{\mathrm{3}}]{\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\frac{\mathrm{6}}{{x}}+\frac{\mathrm{1}}{\:\sqrt{{x}}}−\mathrm{1}}{\mathrm{8}−\frac{\mathrm{4}}{{x}}}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 28/Sep/20
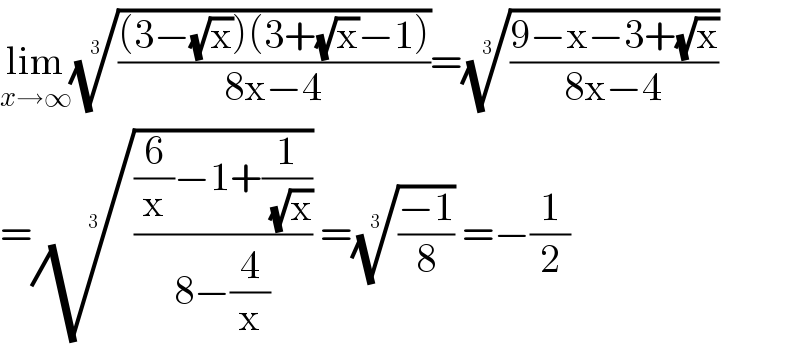
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt[{\mathrm{3}}]{\frac{\left(\mathrm{3}−\sqrt{\mathrm{x}}\right)\left(\mathrm{3}+\sqrt{\mathrm{x}}−\mathrm{1}\right)}{\mathrm{8x}−\mathrm{4}}}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{9}−\mathrm{x}−\mathrm{3}+\sqrt{\mathrm{x}}}{\mathrm{8x}−\mathrm{4}}} \\ $$$$=\sqrt[{\mathrm{3}}]{\frac{\frac{\mathrm{6}}{\mathrm{x}}−\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}}}}{\mathrm{8}−\frac{\mathrm{4}}{\mathrm{x}}}}\:=\sqrt[{\mathrm{3}}]{\frac{−\mathrm{1}}{\mathrm{8}}}\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
