Question Number 154081 by iloveisrael last updated on 14/Sep/21
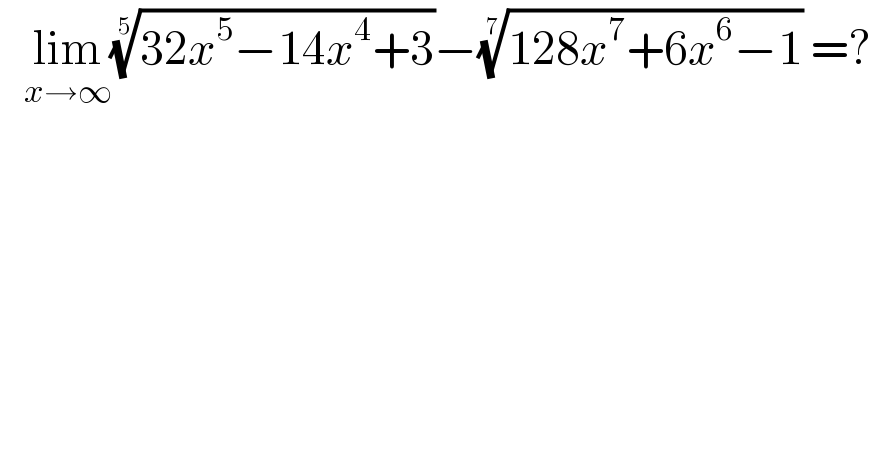
$$\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt[{\mathrm{5}}]{\mathrm{32}{x}^{\mathrm{5}} −\mathrm{14}{x}^{\mathrm{4}} +\mathrm{3}}−\sqrt[{\mathrm{7}}]{\mathrm{128}{x}^{\mathrm{7}} +\mathrm{6}{x}^{\mathrm{6}} −\mathrm{1}}\:=? \\ $$
Answered by EDWIN88 last updated on 14/Sep/21
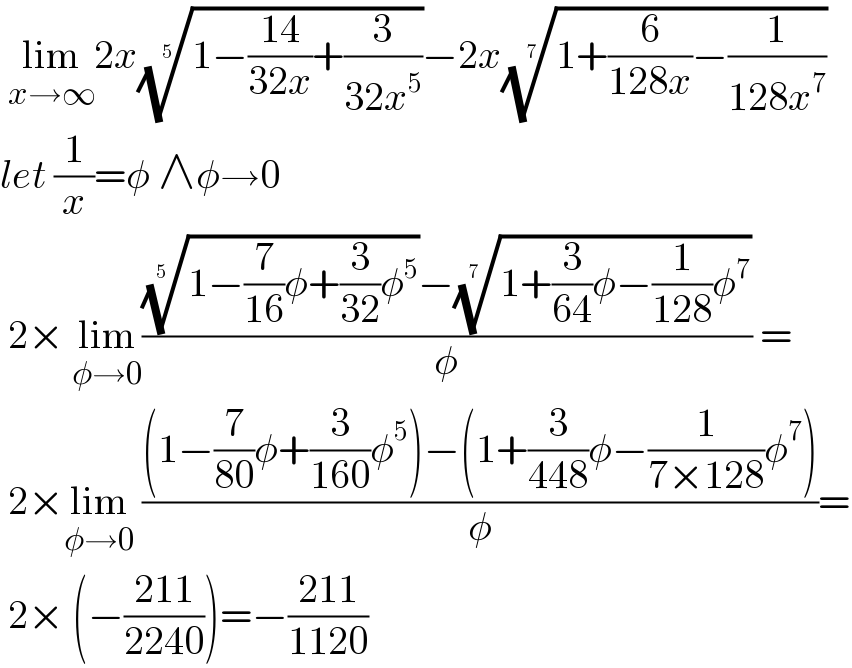
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}2}{x}\sqrt[{\:\mathrm{5}}]{\mathrm{1}−\frac{\mathrm{14}}{\mathrm{32}{x}}+\frac{\mathrm{3}}{\mathrm{32}{x}^{\mathrm{5}} }}−\mathrm{2}{x}\sqrt[{\mathrm{7}}]{\mathrm{1}+\frac{\mathrm{6}}{\mathrm{128}{x}}−\frac{\mathrm{1}}{\mathrm{128}{x}^{\mathrm{7}} }} \\ $$$${let}\:\frac{\mathrm{1}}{{x}}=\phi\:\wedge\phi\rightarrow\mathrm{0} \\ $$$$\:\mathrm{2}×\:\underset{\phi\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{5}\:}]{\mathrm{1}−\frac{\mathrm{7}}{\mathrm{16}}\phi+\frac{\mathrm{3}}{\mathrm{32}}\phi^{\mathrm{5}} }−\sqrt[{\mathrm{7}\:}]{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{64}}\phi−\frac{\mathrm{1}}{\mathrm{128}}\phi^{\mathrm{7}} }}{\phi}\:= \\ $$$$\:\mathrm{2}×\underset{\phi\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}−\frac{\mathrm{7}}{\mathrm{80}}\phi+\frac{\mathrm{3}}{\mathrm{160}}\phi^{\mathrm{5}} \right)−\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{448}}\phi−\frac{\mathrm{1}}{\mathrm{7}×\mathrm{128}}\phi^{\mathrm{7}} \right)}{\phi}= \\ $$$$\:\mathrm{2}×\:\left(−\frac{\mathrm{211}}{\mathrm{2240}}\right)=−\frac{\mathrm{211}}{\mathrm{1120}} \\ $$
