Question Number 149346 by Study last updated on 04/Aug/21
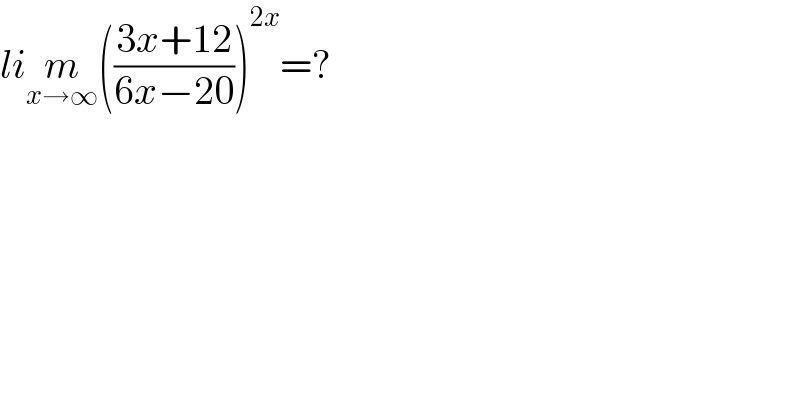
$${li}\underset{{x}\rightarrow\infty} {{m}}\left(\frac{\mathrm{3}{x}+\mathrm{12}}{\mathrm{6}{x}−\mathrm{20}}\right)^{\mathrm{2}{x}} =? \\ $$
Commented by Study last updated on 04/Aug/21

$${helpe}\:{me} \\ $$
Answered by gsk2684 last updated on 04/Aug/21
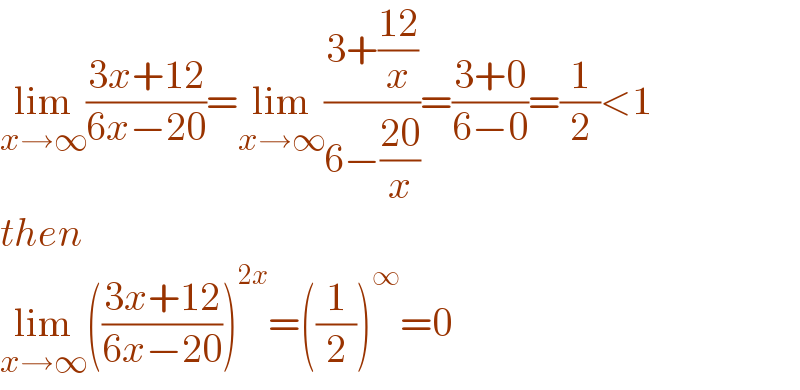
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{3}{x}+\mathrm{12}}{\mathrm{6}{x}−\mathrm{20}}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{3}+\frac{\mathrm{12}}{{x}}}{\mathrm{6}−\frac{\mathrm{20}}{{x}}}=\frac{\mathrm{3}+\mathrm{0}}{\mathrm{6}−\mathrm{0}}=\frac{\mathrm{1}}{\mathrm{2}}<\mathrm{1} \\ $$$${then} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{3}{x}+\mathrm{12}}{\mathrm{6}{x}−\mathrm{20}}\right)^{\mathrm{2}{x}} =\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\infty} =\mathrm{0} \\ $$
Answered by puissant last updated on 04/Aug/21
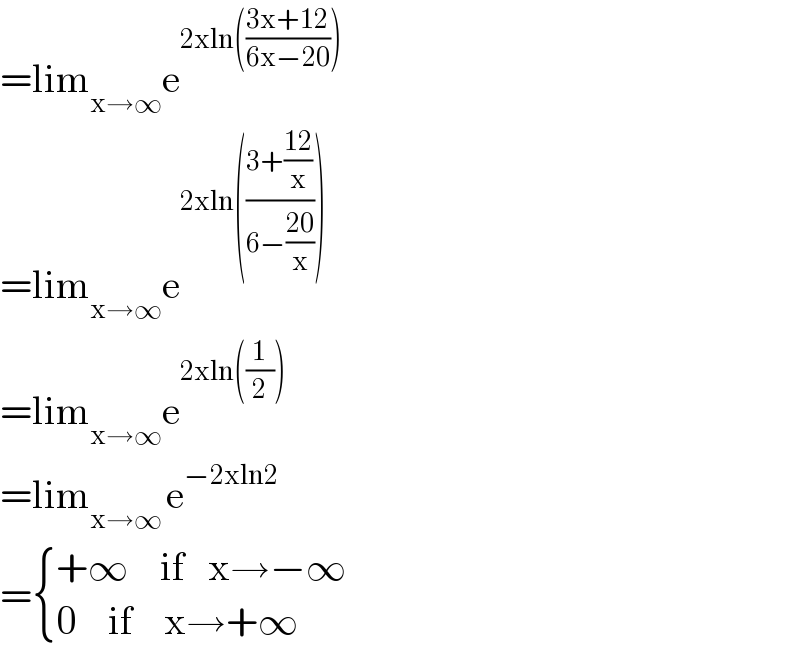
$$=\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \mathrm{e}^{\mathrm{2xln}\left(\frac{\mathrm{3x}+\mathrm{12}}{\mathrm{6x}−\mathrm{20}}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \mathrm{e}^{\mathrm{2xln}\left(\frac{\mathrm{3}+\frac{\mathrm{12}}{\mathrm{x}}}{\mathrm{6}−\frac{\mathrm{20}}{\mathrm{x}}}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \mathrm{e}^{\mathrm{2xln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\infty\:} \mathrm{e}^{−\mathrm{2xln2}} \\ $$$$=\begin{cases}{+\infty\:\:\:\:\mathrm{if}\:\:\:\mathrm{x}\rightarrow−\infty}\\{\mathrm{0}\:\:\:\:\mathrm{if}\:\:\:\:\mathrm{x}\rightarrow+\infty}\end{cases} \\ $$
