Question Number 83323 by john santu last updated on 01/Mar/20
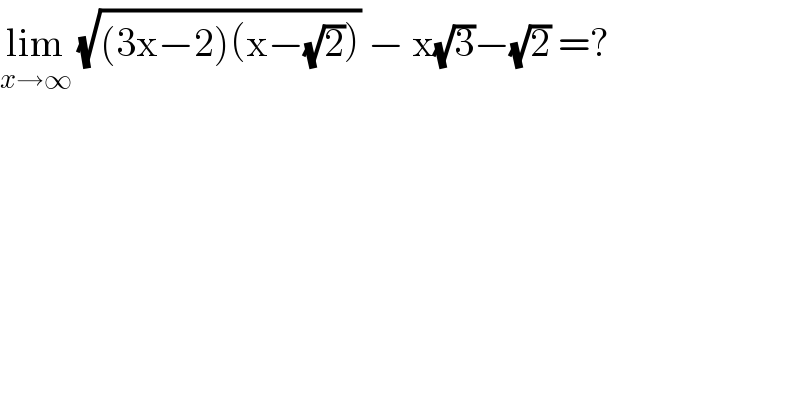
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\left(\mathrm{3x}−\mathrm{2}\right)\left(\mathrm{x}−\sqrt{\mathrm{2}}\right)}\:−\:\mathrm{x}\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\:=? \\ $$$$ \\ $$
Commented by abdomathmax last updated on 01/Mar/20
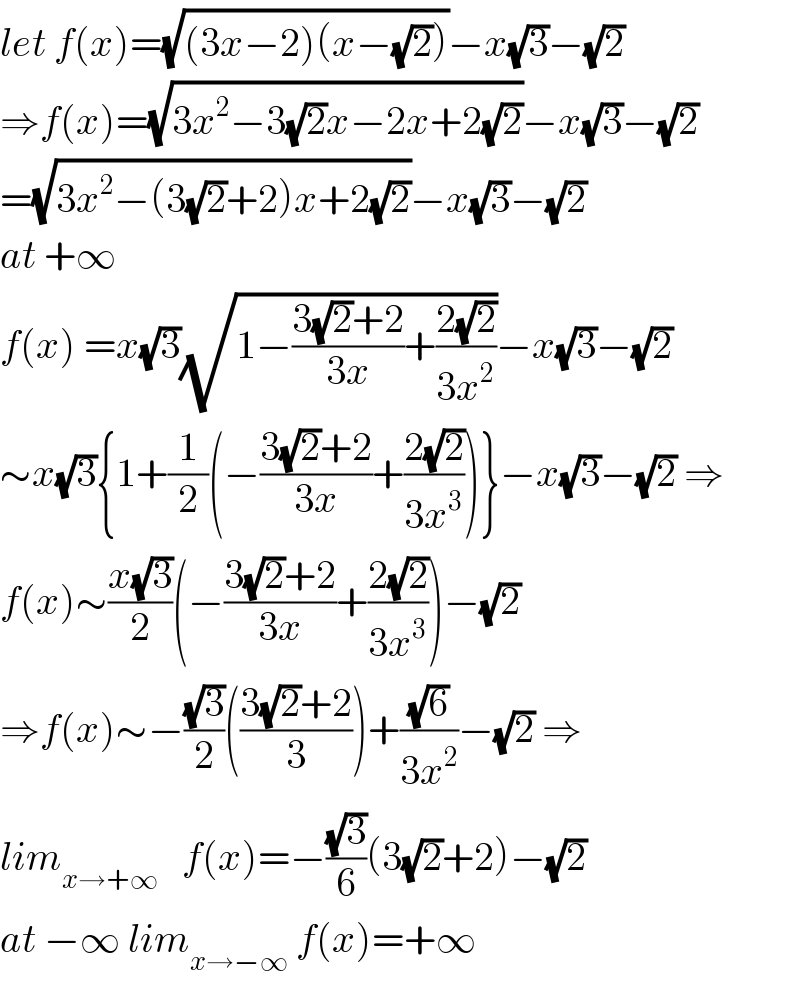
$${let}\:{f}\left({x}\right)=\sqrt{\left(\mathrm{3}{x}−\mathrm{2}\right)\left({x}−\sqrt{\mathrm{2}}\right)}−{x}\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{f}\left({x}\right)=\sqrt{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}\sqrt{\mathrm{2}}{x}−\mathrm{2}{x}+\mathrm{2}\sqrt{\mathrm{2}}}−{x}\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}} \\ $$$$=\sqrt{\mathrm{3}{x}^{\mathrm{2}} −\left(\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}\right){x}+\mathrm{2}\sqrt{\mathrm{2}}}−{x}\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}} \\ $$$${at}\:+\infty \\ $$$${f}\left({x}\right)\:={x}\sqrt{\mathrm{3}}\sqrt{\mathrm{1}−\frac{\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}}{\mathrm{3}{x}}+\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}{x}^{\mathrm{2}} }}−{x}\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}} \\ $$$$\sim{x}\sqrt{\mathrm{3}}\left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}}{\mathrm{3}{x}}+\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}{x}^{\mathrm{3}} }\right)\right\}−{x}\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\frac{{x}\sqrt{\mathrm{3}}}{\mathrm{2}}\left(−\frac{\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}}{\mathrm{3}{x}}+\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}{x}^{\mathrm{3}} }\right)−\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{f}\left({x}\right)\sim−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\frac{\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}}{\mathrm{3}}\right)+\frac{\sqrt{\mathrm{6}}}{\mathrm{3}{x}^{\mathrm{2}} }−\sqrt{\mathrm{2}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow+\infty} \:\:\:{f}\left({x}\right)=−\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\left(\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}\right)−\sqrt{\mathrm{2}} \\ $$$${at}\:−\infty\:{lim}_{{x}\rightarrow−\infty} \:{f}\left({x}\right)=+\infty \\ $$
Answered by jagoll last updated on 01/Mar/20
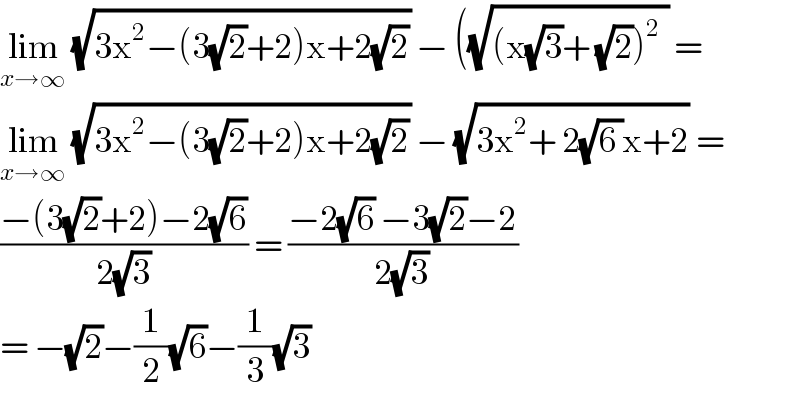
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{3x}^{\mathrm{2}} −\left(\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}\right)\mathrm{x}+\mathrm{2}\sqrt{\mathrm{2}}}\:−\:\left(\sqrt{\left(\mathrm{x}\sqrt{\mathrm{3}}+\:\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:}\:=\right. \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{3x}^{\mathrm{2}} −\left(\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}\right)\mathrm{x}+\mathrm{2}\sqrt{\mathrm{2}}}\:−\:\sqrt{\mathrm{3x}^{\mathrm{2}} +\:\mathrm{2}\sqrt{\mathrm{6}\:}\mathrm{x}+\mathrm{2}}\:= \\ $$$$\frac{−\left(\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}\right)−\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{2}\sqrt{\mathrm{3}}}\:=\:\frac{−\mathrm{2}\sqrt{\mathrm{6}}\:−\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$=\:−\sqrt{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\mathrm{3}} \\ $$
Commented by john santu last updated on 01/Mar/20

$$\mathrm{good}\:\mathrm{sir} \\ $$
