Question Number 174492 by naka3546 last updated on 02/Aug/22
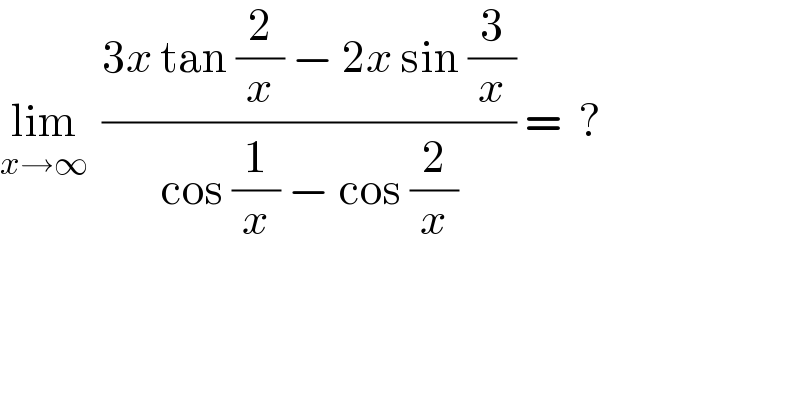
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\frac{\mathrm{3}{x}\:\mathrm{tan}\:\frac{\mathrm{2}}{{x}}\:−\:\mathrm{2}{x}\:\mathrm{sin}\:\frac{\mathrm{3}}{{x}}}{\mathrm{cos}\:\frac{\mathrm{1}}{{x}}\:−\:\mathrm{cos}\:\frac{\mathrm{2}}{{x}}}\:=\:\:? \\ $$
Commented by kaivan.ahmadi last updated on 02/Aug/22

$${we}\:{use}\:{Taylor}\:{series} \\ $$$$\sim{li}\underset{{x}\rightarrow\infty} {{m}}\:\frac{\mathrm{3}{x}\left(\frac{\mathrm{2}}{{x}}−\frac{\mathrm{8}}{\mathrm{3}{x}^{\mathrm{3}} }\right)−\mathrm{2}{x}\left(\frac{\mathrm{3}}{{x}}−\frac{\mathrm{9}}{\mathrm{2}{x}^{\mathrm{3}} }\right)}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{24}{x}^{\mathrm{4}} }\right)−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{3}{x}^{\mathrm{4}} }\right)} \\ $$$$ \\ $$$$={li}\underset{{x}\rightarrow\infty} {{m}}\:\frac{−\frac{\mathrm{8}}{{x}^{\mathrm{2}} }+\frac{\mathrm{9}}{{x}^{\mathrm{2}} }}{\frac{\mathrm{1}}{\mathrm{24}{x}^{\mathrm{4}} }−\frac{\mathrm{2}}{\mathrm{3}{x}^{\mathrm{4}} }}= \\ $$$$ \\ $$$${li}\underset{{x}\rightarrow\infty} {{m}}\:\frac{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\frac{−\mathrm{15}}{\mathrm{24}{x}^{\mathrm{4}} }}={li}\underset{{x}\rightarrow\infty} {{m}}\:\frac{\mathrm{24}{x}^{\mathrm{2}} }{−\mathrm{15}}=−\infty \\ $$$$ \\ $$$$ \\ $$
