lim-x-4-asin-x-4-cos-pix-1-x-4-x-2-x-3-4-Find-a-

Question Number 35939 by rahul 19 last updated on 26/May/18

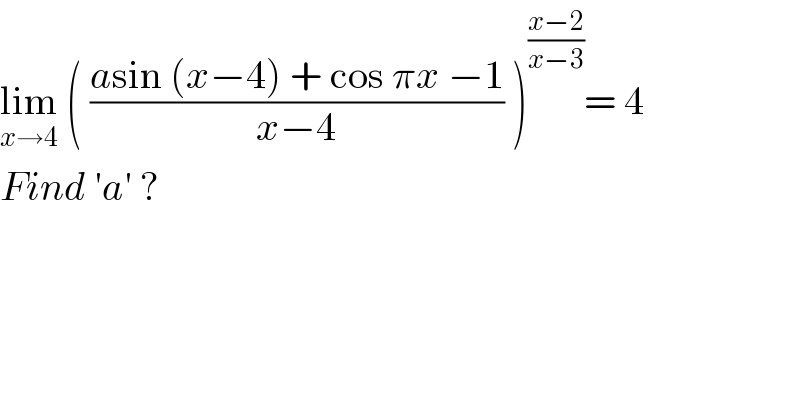
lim_(x→4) ( ((asin (x−4) + cos πx −1)/(x−4)) )^((x−2)/(x−3)) = 4 Find ′a′ ?

$$\underset{{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\:\left(\:\frac{{a}\mathrm{sin}\:\left({x}−\mathrm{4}\right)\:+\:\mathrm{cos}\:\pi{x}\:−\mathrm{1}}{{x}−\mathrm{4}}\:\right)^{\frac{{x}−\mathrm{2}}{{x}−\mathrm{3}}} =\:\mathrm{4} \\ $$$${Find}\:'{a}'\:? \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 26/May/18

t=x−4 ((lim)/(t→0))×{((asint+cosΠ(t+4)−1)/t)}^((t+2)/(t+1)) =((lim)/(t→0))×{((asint+cosΠt−1)/t)}^((t+2)/(t+1)) =((lim)/(t→0))×{((asint)/t)−((2sin^2 (((Πt)/2)))/t)}^((t+2)/(t+1)) =((lim)/(t→0))×{((asint)/t)−2((sin(((Πt)/2)))/((((Πt)/2))))×(Π/2)×sin((Πt)/2)}^((t+2)/(t+1)) =a^2 so a^2 =4 a±2

$${t}={x}−\mathrm{4} \\ $$$$\frac{{lim}}{{t}\rightarrow\mathrm{0}}×\left\{\frac{{asint}+{cos}\Pi\left({t}+\mathrm{4}\right)−\mathrm{1}}{{t}}\right\}^{\frac{{t}+\mathrm{2}}{{t}+\mathrm{1}}} \\ $$$$=\frac{{lim}}{{t}\rightarrow\mathrm{0}}×\left\{\frac{{asint}+{cos}\Pi{t}−\mathrm{1}}{{t}}\right\}^{\frac{{t}+\mathrm{2}}{{t}+\mathrm{1}}} \\ $$$$=\frac{{lim}}{{t}\rightarrow\mathrm{0}}×\left\{\frac{{asint}}{{t}}−\frac{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\Pi{t}}{\mathrm{2}}\right)}{{t}}\right\}^{\frac{{t}+\mathrm{2}}{{t}+\mathrm{1}}} \\ $$$$=\frac{{lim}}{{t}\rightarrow\mathrm{0}}×\left\{\frac{{asint}}{{t}}−\mathrm{2}\frac{{sin}\left(\frac{\Pi{t}}{\mathrm{2}}\right)}{\left(\frac{\Pi{t}}{\mathrm{2}}\right)}×\frac{\Pi}{\mathrm{2}}×{sin}\frac{\Pi{t}}{\mathrm{2}}\right\}^{\frac{{t}+\mathrm{2}}{{t}+\mathrm{1}}} \\ $$$$={a}^{\mathrm{2}} \\ $$$${so}\:{a}^{\mathrm{2}} =\mathrm{4}\:\:\:{a}\pm\mathrm{2} \\ $$

Commented by rahul 19 last updated on 26/May/18

Is a=-2 acceptable ?

Commented by rahul 19 last updated on 26/May/18

$${Thank}\:{You}\:{sir}. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 26/May/18

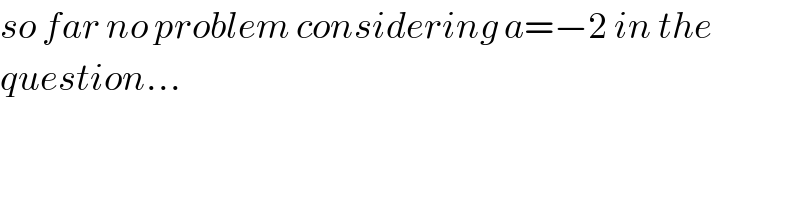
so far no problem considering a=−2 in the question...

$${so}\:{far}\:{no}\:{problem}\:{considering}\:{a}=−\mathrm{2}\:{in}\:{the}\: \\ $$$${question}… \\ $$

Commented by Joel579 last updated on 26/May/18

Sir Tanmay, you can tap the ′sin′ button next to the ′SEL′ button, and then press ′lim_(x→0) ′ button It′s just tips so you won′t type limit manually

$$\mathrm{Sir}\:\mathrm{Tanmay},\:\mathrm{you}\:\mathrm{can}\:\mathrm{tap}\:\mathrm{the}\:'\mathrm{sin}'\:\mathrm{button}\:\mathrm{next}\:\mathrm{to} \\ $$$$\mathrm{the}\:'\mathrm{SEL}'\:\mathrm{button},\:\mathrm{and}\:\mathrm{then}\:\mathrm{press}\:\:'\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:'\:\:\mathrm{button} \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{just}\:\mathrm{tips}\:\mathrm{so}\:\mathrm{you}\:\mathrm{won}'\mathrm{t}\:\mathrm{type}\:\mathrm{limit}\:\mathrm{manually} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 26/May/18

$${thank}\:{you}\:{sir}.. \\ $$

Facebook Tweet Pin

lim-x-4-asin-x-4-cos-pix-1-x-4-x-2-x-3-4-Find-a-

Leave a Reply Cancel reply